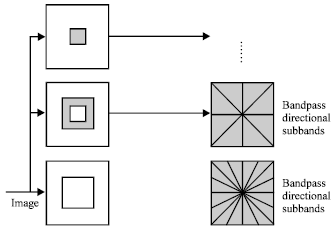
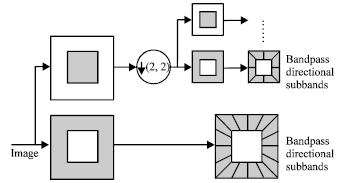
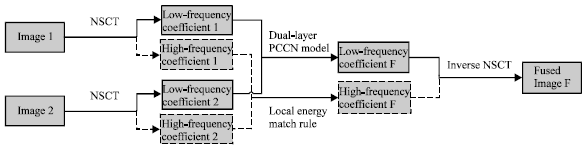
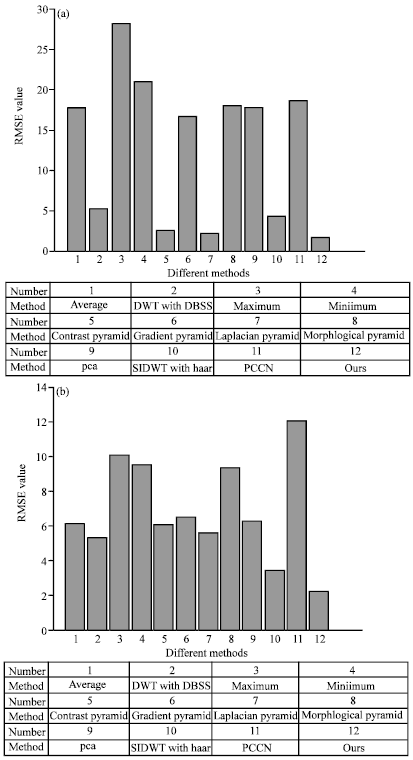
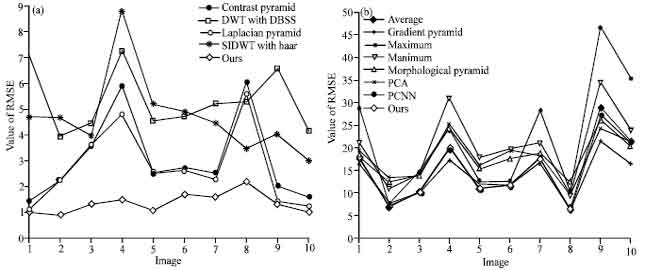
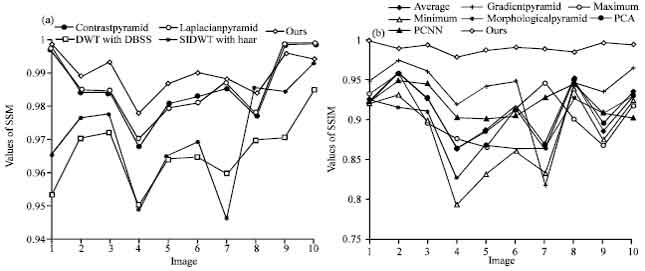
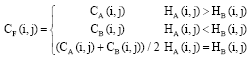Research Article
Multi-focus Image Fusion Based on The Nonsubsampled Contourlet Transform and Dual-layer PCNN Model
School of Information Science and Engineering, Central South University, Changsha, 410083, China
Beiji Zou
School of Information Science and Engineering, Central South University, Changsha, 410083, China
Jianfeng Li
School of Information Science and Engineering, Central South University, Changsha, 410083, China
Yixiong Liang
School of Information Science and Engineering, Central South University, Changsha, 410083, China