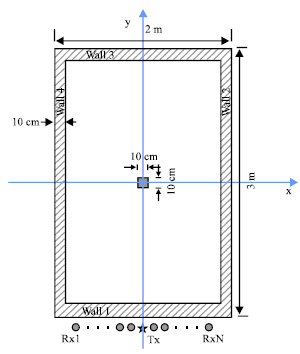
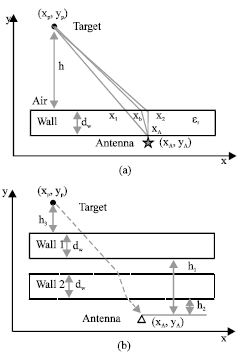
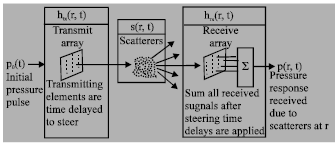
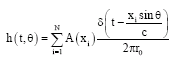Research Article
Impulse Radio Ultra-Wide-Band Through Wall Imaging Radar Based on Multiple-Input Multiple-Output Antenna Arrays
Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, 518055, China
Z. Qin-Yu
Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, 518055, China