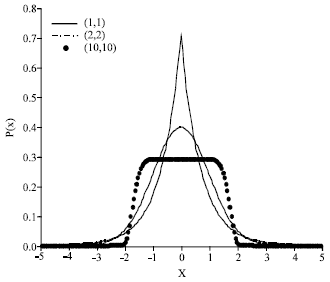
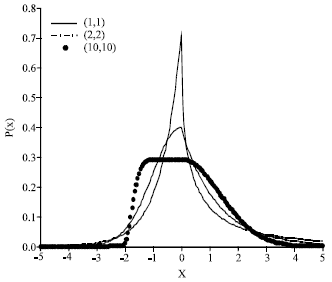
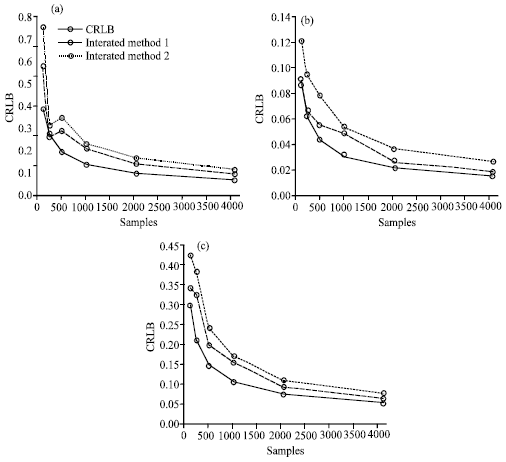
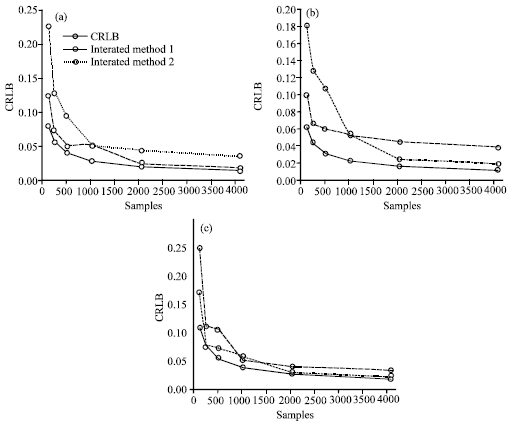
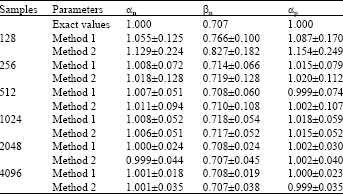
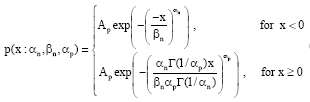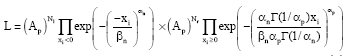Research Article
Parameter Estimation of the Extended Generalized Gaussian Family Distributions using Maximum Likelihood Scheme
Department of Marine Engineering, National Kaohsiung Marine University, 482, Chung-Chou 3rd Road, Chi-Jin District, Kaohsiung 805, Taiwan