Research Article
Empirical Mode Decomposition for BER Improvement in Cellular Network
Department of Electronics and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
Z. Xu
Department of Electronics and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
F. Wang
Department of Electronics and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
B. Huang
Department of Electronics and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China









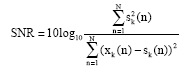
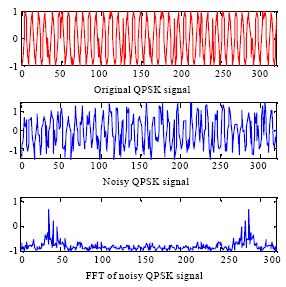
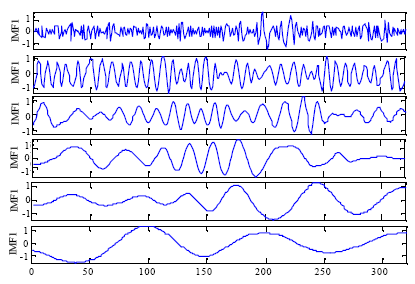
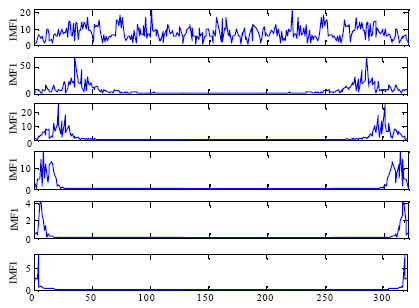
Sapan Mankad Reply
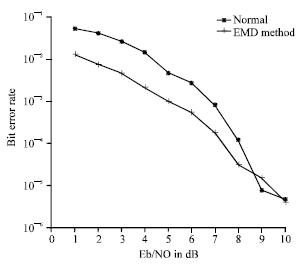
I read the paper and found it very useful.I would certainly like to work on this area.IMF is very useful concept to analyze signals.