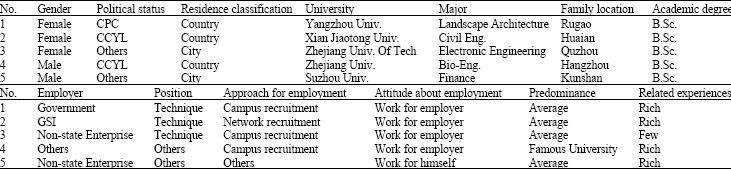
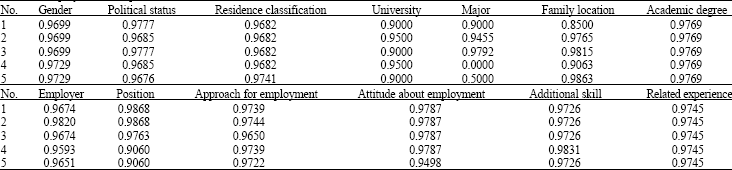
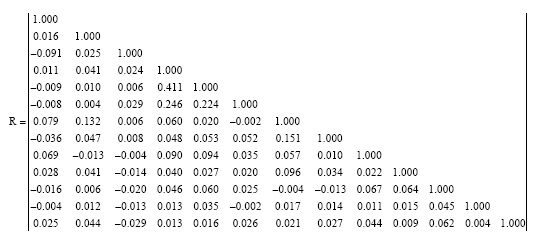
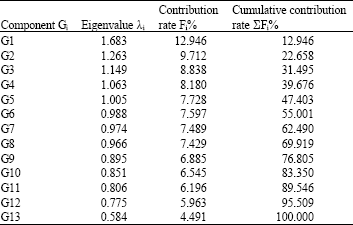
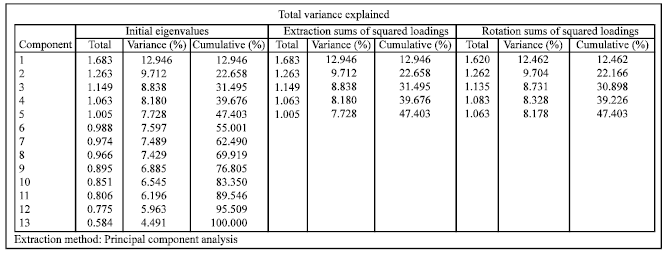
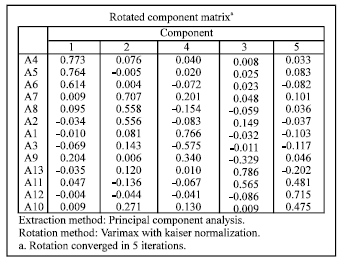
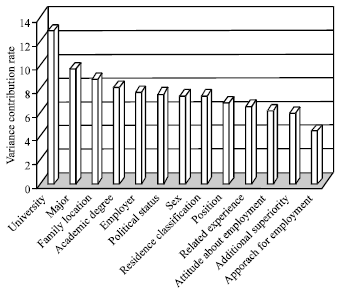
Research Article
Statistical Study on Principal Factors Affecting Employment of Chinese Undergraduates
College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310032, China
W. Zhuge
College of Foreign Language, Hangzhou Dianzi University, Hangzhou, China
K. Zhou
College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310032, China
L. Meng
College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310032, China