Research Article
Taguchi Optimization of Multi-Objective CNC Machining Using TOPSIS
Department of Information Management, Yu Da College of Business, Miaoli County, Taiwan 361, Republic of China
Surface roughness, tool life and cutting force are commonly considered as manufacturing goals (Davim and Conceicao Antonio, 2001) for turning operations in many of the existing researches (Nian et al., 1999). It is also recognized that lighter cutting force often results to better surface roughness and tool life. This is why smaller cutting conditions conclude toward to be optimum (Lin et al., 2001a). As the flexibility and adaptability needs increased, the stability of modern CNC machines is now designed robust. Since, the productivity concern becomes more critical than the cutting force in the industry, the Material Removal Rate (MRR) is more to be concerned than the cutting force.
As the CNC (computer numerical controlled) machines play a major role in modern machining industry, the product quality as well as productivity become important issues. The machining process on a CNC (computer numerical controlled) lathe is programmed by speed, feed rate and cutting depth, which are frequently determined based on the job shop experiences. However, the machine performance and the product characteristics are not guaranteed to be acceptable. Therefore, the optimum turning conditions have to be accomplished. Therefore, the optimum turning conditions have to be accomplished. It is mentioned that the tool nose run-off will affect the performance of the machining process (Yeh, 1994). To reduce the costly and time-consuming experiments, this study employs the tool wear ratio (tool wear length per unit material removal volume) instead of the tool life (Galante et al., 1998) to demonstrate the tool wear status of turning under specific parameter combination.
Among the existing parametric optimization researches on turning conditions, Lin et al. (2001b) have constructed simulation models for surface roughness and cutting forces using convergence network. Davim and Conceicao Antonio (2001) have developed mathematical models to express cutting force as functions of surface roughness and tool life and then optimize the turning parameters by using GA (genetic algorithm) (Ko and Kim, 1998). Nevertheless, these are regarded as computing simulations and the applicability to real world industry is still uncertain. Parameter optimization for multiple attributes is a hard-solving issue because of the interactions between parameters. Problems related to the enhancement of product quality and production efficiency can always be related to the optimization procedures. Taguchi method (Anastasiou, 2002), an experimental design method, has been widely applied to many industries. It can not only optimize quality characteristics through the setting of design parameters, but also reduce the sensitivity of the system performance to variable sources (Huh et al., 2003; Kim et al., 2003). The Taguchi method adopts a set of orthogonal arrays to investigate the effect of parameters on specific quality characteristics to decide the optimum parameter combination. These kinds of arrays use a small number of experimental runs to analyze the quality effects of parameters as well as the optimum combination of parameters.
With all the viewpoints above, this study proposes an optimization approach using orthogonal array and TOPSIS (technique for order preference by similarity to ideal solution) (Hwang and Yoon, 1981), a multi-objective integration technique, to optimize precision CNC turning conditions. Therefore, the optimum multi-objective cutting parameters can then be achieved through the analysis of factor responses in the Taguchi experiment. The results definitely contribute the optimum solution of compromising technique for multiple precision CNC turning objectives with profound insight.
This study is conducted in Yu Da College of Business and as a graduate student’s thesis since August 2008 to July 2009.
Essentially, traditional experimental design procedures are too complicated and not easy to use. A large number of experimental studies have to be carried out when the number of the process parameters increases. To solve this problem, the Taguchi method uses a special design of orthogonal arrays to study the entire parameter space with only a small number of experiments (Yang and Tang, 1998). In this study, the parameter optimization technique and multi-objective integration for CNC turning operations are proposed using Taguchi method (Palanikumar, 2008; Ross, 1998) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), respectively.
Taguchi method: The Taguchi method is a robust design method technique (Palanikumar, 2008; Ross, 1998), which provides a simple way to design an efficient and cost effective experiment. In order to efficiently reduce the numbers of conventional experimental tasks, the orthogonal array (Chang, 2000; Wei et al., 2002) by using design parameters (control factors) in column and standard quantities (levels) in row is proposed and further adopted in this study. The performance measure, signal to noise ratio (S/N) (Park et al., 2005) proposed by Taguchi is used to obtain the optimum parameter combinations. The larger S/N means the relation to the quality will become better. The lower quality characteristic will be regarded as a better result when considering the smaller-the-best quality. The related S/N ratio is defined as:
| (1) |
where, n is the number of experiments for each experimental set and y1 expresses the quality characteristic at the ith experiment.
On the contrary, the larger quality characteristic will have better result t when considering the larger-the-best quality, therefore, by taking the inverse of quality characteristic into Eq. 1, the related S/N ratio can also be deduced and shown in Eq. 2.
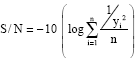 | (2) |
Integration of multiple objectives: Hwang and Yoon (1981) developed TOPSIS (technique for order preference by similarity to ideal solution) to assess the alternatives before multiple-attribute decision making. TOPSIS considers simultaneously the distance to the ideal solution and negative ideal solution regarding each alternative and also selects the most relative closeness to the ideal solution as the best alternative (Tong et al., 2005).
When the alternative set for multi-attribute decision and evaluation attribute set are described as A = {ai|| i = 1, 2,….,m} and {g = gi|| j = 1, 2,….,n}, respectively; the computational steps of TOPSIS can be expressed as:
Step 1:This step involves a matrix based on all the information available that describes a material’s attributes and is called a decision matrix. Each row of this matrix is allocated to one alternative and each column to one attribute. The decision matrix can be stated as:
 | (3) |
where, Ai represents the possible alternatives, i = 1, 2,….,m; Xj denotes the attributes relating to alternative performance, j = 1, 2…..,n and xij is the performance of Ai with respect to attribute Xj.
Step 2:Obtain the normalized decision matrix rij. This can be represented as:
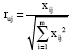 | (4) |
where, rij represents the normalized performance of Ai with respect to attribute Xj.
Step 3:Assume that the weight of each attribute is {wj|| j = 1, 2,….,n}, the weighted normalized decision matrix V = [vij] can be found as:
| (5) |
Where:
Step 4:Develop the ideal (best) and negative ideal (worst) solutions in this step. The ideal and negative ideal solution can be expressed as:
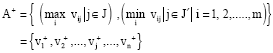 | (6) |
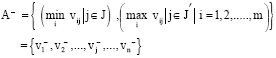 | (7) |
Where:
| J | = | {j = 1, 2,…,n| j}:Associated with the beneficial attributes |
| J' | = | {j = 1, 2,…,n| j}:Associated with non-beneficial attributes |
Step 5:Determine the distance measures. The separation of each alternative from the ideal one is given by n-dimensional Euclidean distance from the following equations:
| (8) |
| (9) |
Step 6:The proximity of a particular alternative to the ideal solution is expressed in this step as follows:
| (10) |
Step 7:A set of alternatives is made in descending order according to the preference value indicating the most preferred and least preferred feasible solutions.
In this study, the overall relational rating using TOPSIS for multiple precision CNC machining objectives is introduced to the Taguchi experiment as the S/N ratio. Therefore, it is judged as the quality of larger-the-best. In addition to the S/N ratio, a statistical Analysis of Variance (ANOVA) (Wu and Chyu, 2002) can be employed to indicate the impact of process parameters. In this way, the optimal levels of process parameters can be estimated.
RESEARCH DESIGN
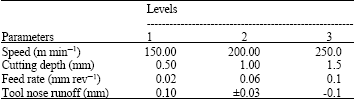
Surface roughness, tool wear and Material Removal Rate (MRR) are considered major attributes in this study. Four parameters with three levels are selected to optimize the multi-attribute finish turning based on the L9(34) orthogonal array. The precision diameter turning operation of S45C (φ45x250 mm) work piece on an ECOCA-3807 CNC lathe is arranged for the research. The TOSHIBA WTJNR2020K16 tool holder with MITSUBISHI NX2525 insert is utilized as the cutting tool. The design is shown as follows.
Experimental setup: The surface roughness (Ra) of machined work pieces are measured on the MITSUTOYO SURFTEST. The surface roughness of each work piece is measured 4 times at 3 different sections of 40, 80 and 120 mm from the face. Through, the measurement of surface roughness on the nine work pieces, the average data are received. The tool wearing length VB2 (mm) in Fig. 1 is scaled on the 3D SONY COLOR VIDEO electronic camera. The tool wearing length is then divided by the volume of material removed as the tool wear ratio (mm-2), which is utilized as the indicator of tool wear in this study. And the MRR (mm3 min-1) is calculated using the following equation.
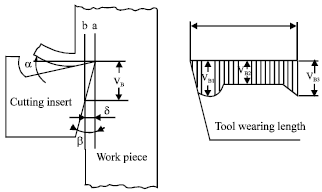 | |
| Fig. 1: | Tool wear length |
| Table 1: | Parameters and levels |
 | |
| Table 2: | The L9(34) experimental setup |
 | |
| (11) |
In Eq. 11, f (mm revolution-1) denotes the feed rate, d (mm) describes the cutting depth and v (m min-1) presents the surface speed of the turning operation.
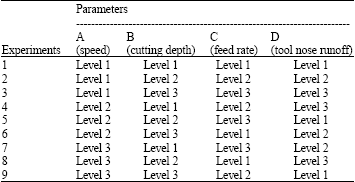
Construction of orthogonal array: In this study, the four turning parameters (cutting depth, feed rate, speed and tool nose runoff) with three different levels (Table 1) are experimentally constructed for the machining operation. In Table 1, the three levels of cutting depth, feed rate and speed are identified from the machining handbook suggested by the tool manufacturer. The tool nose runoff is positioned by using different shims located under the tool holder and determined by measuring the tip after face turned the work piece. When the tool nose is set approximately 0.1 mm higher (lower) than the center of the work piece, it is regarded as level 1 (level 3). When the tool nose is set within ±0.03 mm, it is considered as level 2. The orthogonal array is then selected to perform the nine sets of machining experiments. The parameter levels for the experiments are shown in Table 2.
In this study, each work piece is diameter turned 150 mm in length from the face with three passes using a brand new cutting edge of the insert. The experimental results are described as follows:
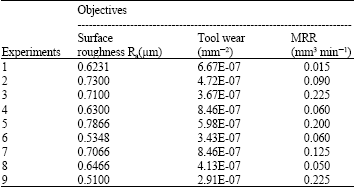
Multi-objective optimization results: By considering the parameter combinations of the nine sets of experiment based on the L9(34) orthogonal array, the machining objectives are determined and shown in Table 3. With the machined results based on the orthogonal array, the preference value for each experiment combination by using TOPSIS can then be achieved and shown in Table 4.
| Table 3: | Experimental results |
 | |
| Table 4: | Preference value |
 | |
| Table 5: | Confirmation results |
 | |
Introducing the relational rating as the signal to noise ratio (S/N) of multiple machining objectives for larger-the-best expectation, the results of factor responses are calculated. The mean effects for S/N ratios (Fig. 2A-D) are then drawn by MINITAB 14. Therefore, the optimum multi-objective turning parameters are found to be A3 (250 m min-1), B3 (1.5 mm), C3 (0.1 mm rev-1), D1 (0.1 mm).
Discussion of the optimality: To verify the optimality of the optimum result achieved by the proposed multi-objective optimization technique, the machining operations under both multi-objective optimum parameters (A3B3C3D1) and benchmark parameters (A2B2C2D2), which are often introduced into the confirmation experiment in many of the studies (Tosun and Ozler, 2004; Lin and Lin, 2006) for comparison to the optimum parameters, are performed on the CNC lathe. From Table 5, it is observed that the surface roughness and tool wear ratio are improved by 27.80 and 16.21%, respectively. And the MRR under optimum parameters is greatly increasing about 212.5%. The preference value is also improved by 39.69%.
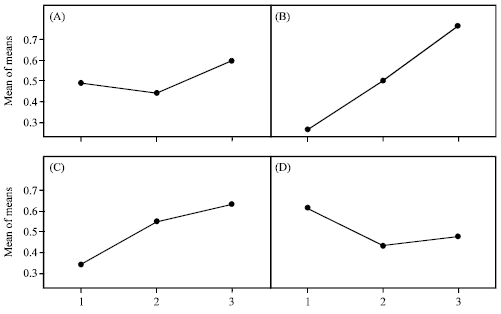 | |
| Fig. 2: | (A-D) Plot of main effects for means |
In this study, the Taguchi optimization and TOPSIS were applied to achieve the optimum process parameters of CNC turning under the considerations of multiple objectives. A validation experiment within the optimum parameters was conducted to indicate the effectiveness of the proposed optimization method. Through, the validation test, the experimental results verify the effectiveness of this study. With the experimental results, it is found that the surface roughness and tool wear ratio are improved by 27.80 and 16.21%, respectively. And the MRR under optimum parameters is greatly increasing about 212.5%. The preference value is also improved by 39.69%.
Parametric optimization is a hard-solving matter because of the interactions between parameters. This study not only proposes an optimization approach using orthogonal array and TOPSIS, but also contributes the satisfactory technique for improving the multiple machining performances in CNC turning with profound insight.
Financial support for this study was provided by the National Science Council Taiwan, Republic of China, under the contract of NSC97-2221-E-412-003. The author would also like to thank the anonymous referees, who kindly provided the suggestions and comments to improve this study.