Research Article
Using Immune Network in Nonlinear System Identification for a 3D Parallel Robot
Department of Information Management, Yu Da College of Business,Miaoli County, Taiwan 361, Rebublic of China
Nonlinear system identification either forward or inverse model identification is suitable to establish the model of unknown system. Therefore, nonlinear system identification is becoming increasingly important in modern control applications (Babuska et al., 1998; Yu and Li, 2001). Nonlinear system identification can improve control performance significantly, especially when the system behaviors are unknown, complex and with great nonlinearity. In general, the system models can be classified into two groups: physical model is using the physical property to derive the model of system and input-output model is using the relationship between input and output data of the system to establish the model. The first method to establish the model usually must to use the complex mathematic equation to derive the model of system and the model has many limits to follow it then affect the performance of the model. The second method to establish the model is using the relationship between input and output data of system and this is the great advantage of the system identification (Liu and Kadirkamanathan, 1999; Tzes et al., 1998; Venkatesh and Dahleh, 2001).
System identification is used to establish the mathematical model of unknown system. If input and output data of this unknown system can be fulfilled to the model we established, then we called it an approximate model of the unknown system. Nonlinear system identification consists of model structure selection and parameter estimation which are very important. For multivariable (or MIMO) systems, the nonlinear structure could be treated as a link from acquired input and output data to a regression vector from the unknown system. Then, it is to establish the mathematical model of system dynamics and also use few parameters to estimate behavior of the model of nonlinear system.
For nonlinear system identification, NARX model has been implemented in several types of configurations such as genetic programming (Enab, 1995; Hwang et al., 2000; Petridis et al., 1998), neural network (Akhmetov et al., 2001; Li et al., 2000), fuzzy modeling (Lee, 1998; Runkler and Palm, 1996; Sousa and Setnes, 2000; Wang et al., 2000) and polynomial representation (Billings et al., 1989; Korenberg et al., 1988; Leontaritis and Billings, 1985a,b). On the other hand, biological information processing systems such as immune system have been increasingly applied to engineering fields. Recent studies on immune system have clarified that simulated the interactions between various components of the immune system such as the stimulation and suppression chains between various cells or the overall behaviors of the system based on an immunology point of view such as rapidly responding to the presence of foreign material, while quickly stabilizing the immune system. In fact, the immune system has the following features: self-organizing, memory, recognition, adaptive and ability to learning. Therefore, immune system could be applied to nonlinear system identification and provided various feasible ideas for system model with robust and adaptive characteristics. The purpose of this study is using immune network identified nonlinear system’s NARX model. A two-link rigid manipulator simulation is used to evaluate the proposed methodology. Leontaritis and Billings (1985a,b) proposed the scheme of NARX model and it used the relations between input and output data of the system and then to establish the mathematical model of system dynamics and also use this model to predict the behavior of unknown system. In addition, Korenberg et al. (1988) proposed the Orthogonal least squares estimator to decide significant term in the NARX model. Billings et al. (1989) made some fix for the methods of Korenberg and proposed the Forward-regression orthogonal estimator in their study and used this method to identify the MIMO system.
Luh and Wu (1999) proposed a genetic algorithm based on nonlinear autoregressive with exogenous inputs system identification algorithm. It was developed to identify nonlinear system and was successfully applied to both nonlinear continuous-time and discrete-time with acceptable accuracy. And they proposed an operator of truncate mutation to improve greatly the convergence rate in identification process. In addition, Luh and Wu (2000) proposed the inversion control of nonlinear system with an inverse NARX model identification using genetic algorithms. The inverse NARX model is derived by inverting the forward NARX model and identified using genetic algorithms. In their study, both experiment and simulation results demonstrate that the proposed controller provides very good performance in the problems of input estimation and output tracking.
The information processing systems in living organisms can be mainly classified into the following four systems: genetic system, brain-nervous, immune system and endogenous system that to provide various feasible ideas to engineering fields. Besides the endogenous system, the genetic system and the brain-nervous have already been applied to engineering fields by modeling as genetic algorithms and neural networks and they have been widely used in various fields. In addition, the immune system has been increasingly applied to engineering fields. Jerne (1973) foremost proposed the hypothetical of immune network (idiotypic network hypothesis) based on mutually stimulus and suppression between antibodies. The concept of immune network states that the network dynamically maintains the memory using feedback mechanism within network. Based on Jerne’s immune network theory, several theories and mathematical models for immune system have been developed and have already been used in various engineering problems (Endoh et al., 1998; Hightower et al., 1995; Hoffmann, 1989; Hunt and Cooke, 1995).
In recent years, many researches of nonlinear system model establishing have been proposed and have become an essential branch of control theory. The common model building methods are using the physical property to derive the model of system or using neural network to learn the model of system or using the relationship between input and output data of the system to establish the model of system etc. However, all the model types for establishing still have their advantages and disadvantages for system model with robust and adaptive characteristics. Because the immune system’s features it could be applied to nonlinear system identification and provided various feasible ideas for system model with robust and adaptive characteristics.
LITERATURE REVIEW
The immune system protects living bodies from the invading of foreign substances such as viruses, bacteria and other parasites (called antigens) which enter the bloodstream. The main task of the immune system is to detect the antigens by lymphocyte cells and produce the immune response to eliminate antigens, so that it has enabled the human species to survive. The basic components of the biological immune system are macrophages and lymphocytes. The lymphocytes play an important role in all immune responses. The main cells of the immune response introduced as follow:
Phagocytes: The phagocyte is an important type of macrophages. It has surface receptors to detect and destroy invaders (antigens, viruses and bacteria) to the human body. The phagocytes are using primitive non-specific recognition systems to bound and destroy invaders. It is called non-specific immune response as the first line of defense.
Lymphocytes: There are mainly two types of lymphocytes, namely B-lymphocytes (B-cells) and T-lymphocytes (T-cells). B-lymphocytes are the cells produced by bone marrows and T-lymphocytes are the cells produced by thymus. In addition, lymphocytes float freely in blood and lymph node. They patrol everywhere for foreign antigens, then gradually drift into the lymphatic system, to begin the cycle all over again.
The B-cells take part in the humoral immunity that secrete antibodies by the clonal proliferation, namely antibodies. The T-cells are classified into three different types. Among these T-cells, the first and the second types perform to regulate the production of antibodies from B-cells. These are called T-helper cells (TH). The third types of T-cells capture germ cells or cells infected by viruses to kill them and called T-cytotoxic cells (TC). As a result, T-cells are playing a very important role in the regulation of the immune responses. In addition, the most important feature of both B-cells and T-cells is that they have receptor molecules on their surfaces that can recognize antigens. The B-cells receptor interacts with epitopes present on intact antigen molecules. Antigen molecules may be soluble or bound to a surface. The T-Cells Receptor (TCR) interacts only with cell surface molecules. T-cells secrete chemical substances that can kill other cells or promote their growth.
Immune responses: The immune system possesses two types of immune response: innate (or non-adaptive) responses and adaptive immune responses. When an infectious foreign pathogen attacks the human body, the innate immune system is activated as the first line of defense. Innate immunity is not directed in any way towards specific invaders, rather against any pathogens that enter the body. It is called non-adaptive immune responses. The adaptive immune response occurs when the immune system encounters the antigen for the first time and reacts against it. For example, it may produce antibodies by lymphocytes which combine with the antigen to cause its elimination. The adaptive immune response learns about the specificity antigens, thus preparing the body for any further invasion from that same antigen. This learning mechanism creates the immune system’s memory. In addition, the adaptive immune responses can be elicited from an antigen which is similar, although not identical, to the original one which established the memory. Hence, the immune system possesses a content addressable memory.
Figure 1 shows the model describing the relationship between components on the immune system. The macrophage has surface receptors to detect and destroy invaders to the human body. Then, the macrophage becomes an Antigen Presenting Cell (APC) and releases interleukines, a kind of molecules called Major Histocompatibility Complex (MHC) to distinguish a self from other non-self. The APC transfer information about the antigen to T-cells, activating them. Then, T-cells stimulate B-cells, antibodies are produced by B-cells to neutralize antigens. In addition, diversity in the immune system is maintained because the least stimulated B-cells die daily and are replaced by an equal number of completely new B-cells generated by the bone marrow.
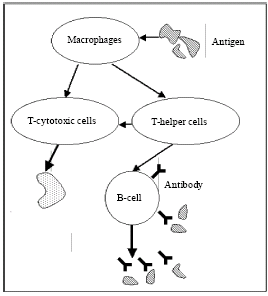 | |
| Fig. 1: | Illustration of the biological immune system |
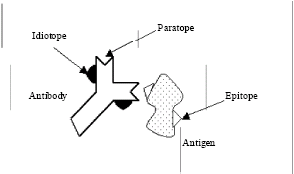 | |
| Fig. 2: | Structure of an antigen and antibody |
These new B-cells are only added to the immune network if they possess an affinity to the cells already in it, otherwise they die.
Immune network: For the sake of convenience of the following explanation, we show the structure of an antigen and antibody in Fig. 2. In Fig. 2, the relationship between an antibody and its corresponding antigen is described. The portion on the antigen recognized by the antibody is called epitope (antigen determinant) and the one on the antibody that recognizes the corresponding antigen determinant is called paratope. On the other hand, each type of antibody has also its specific antigen determinant called idiotope.
Based on antibodies are not just isolated, namely they are communicating to each other among different kinds of antibodies, Jerne (1973) proposed a hypothesis: idiotypic network hypothesis is the concept that the immune system is constructed as a large-scale closed system of lymphocytes paying close attention to mutual interaction between lymphocytes.
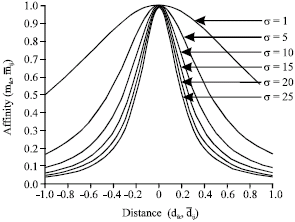 | |
| Fig. 3: | The relation between affinity |
This idea of Jerne’s is schematically shown in Fig. 3. The idiotope Id1 of antibody 1 stimulates the B-lymphocyte 2, which attaches the antibody 2 to its surface, through the paratope P2. With the viewpoint of the antibody 2, the idiotope Id1 of antibody 1 works simultaneously as an antigen. As a result, the B-lymphocyte 1 with the antibodies 1 is suppressed by the antibody 2. On the other hand, the antibody 3 stimulates the antibody 1 since the idiotope Id3 of the antibody 3 works as an antigen for the antibody.
These stimulation and suppression chains between antibodies form the large closed chain loop which works as a self and non-self recognizer.
The main task of the immune system is to detect the antigens by lymphocyte cells and produce the immune response to eliminate antigens. In this study, a novel theory of nonlinear system identification scheme based on NARX immune network is proposed and explain as follow:
Considering a MIMO system can be decomposed as a set of coupled MISO models for system identification. For an r-input-one-output NARX model the equation expand as Eq. 1:
| (1) |
Without loss of generality, it can be simplified as Eq. 2 assuming zero input time delay and identical maximum time lag nlag.
| (2) |
Here,
The regression vector Φ is considered as an epitope of antigen (antigen determinant) and its behavior is the antigen response y (t). Therefore, the total number of antigens will be N!nlag for the whole immune network, where N is the number of data set acquired. In addition, the antibodies in the proposed immune network are defined as below:
| (3) |
where, vector xi is the receptor vector of the ith antibody similar to Φ, includes both paratope and idiotope and ![]() is the corresponding immune response of the ith antibody. NAb is the number of antibodies used in the immune network.
is the corresponding immune response of the ith antibody. NAb is the number of antibodies used in the immune network.
In the whole immune network, the stimulation and suppression chains between antibodies and the matching ratio between the antigen epitope and the antibody receptor are called affinity. In addition, if the paratope and epitope shapes are not quite complementary, then the two molecules may still bind, but with lower affinity. To calculate the affinity mik between ith antibody and kth antibody, the expression can be give as below:
| (4) |
where, ![]() represents the distance between the receptor vectors xi of ith antibody and xk of kth antibody.
represents the distance between the receptor vectors xi of ith antibody and xk of kth antibody.
On the other hand, the following expression is applied to calculate the affinity ![]() between jth antigen and ith antibody.
between jth antigen and ith antibody.
| (5) |
where, ![]() represents the distance between the receptor vectors xi of ith antibody and Φj of jth antigen.
represents the distance between the receptor vectors xi of ith antibody and Φj of jth antigen.
Figure 3 shows the relation between affinity ![]() and distance
and distance![]() associated with different value of σ. Clearly, the larger the value of σ, the wider the area covered by the curve.
associated with different value of σ. Clearly, the larger the value of σ, the wider the area covered by the curve.
For the whole immune network, the immune response ![]() of the ith antibody to the jth antigen is defined as the following equation:
of the ith antibody to the jth antigen is defined as the following equation:
| (6) |
with
| (7) |
where, ![]() is a constant and equal to -1.5 in this study. Under such situation, the immune response of the ith antibody to the jth antigen (i.e.,
is a constant and equal to -1.5 in this study. Under such situation, the immune response of the ith antibody to the jth antigen (i.e., ![]() ) will be of equal value to real output yj if their affinity
) will be of equal value to real output yj if their affinity ![]() is one (which means the receptor of antibody and epitope of antigen are totally matched).
is one (which means the receptor of antibody and epitope of antigen are totally matched).
The dynamic equations of idiotypic network proposed by Jerne (1973) are applied in this study to calculate the concentration of the ith antibody in immune network below:
| (8) |
| (9) |
where, i,k=0,1,…, NAb is a number of antibody, Ai is stimulus of antibody i, ai is the concentration of antibody i, mik is the affinity of antibody i and antibody k, ![]() is the affinity of antigen j and antibody i and ki is natural death coefficient.
is the affinity of antigen j and antibody i and ki is natural death coefficient.
Equation 8 is composed of four terms. The first term is the stimulation between ith antibody and kth antibody. The second term is suppressive interaction between antibodies. The third term is the stimulus from antigen. The final term is natural extinction term represents the dissipation tendency in absence of any interaction.
The stimulated and suppressive relation between antibodies can be integrated as the following affinity matrix Mik:
 | (10) |
where, row vectors represents the antibody i to stimulate the other antibodies and column vectors represents the other antibodies to suppress the antibody i.
Let the error between the real output value yj and immune response ![]() as follow:
as follow:
| (11) |
If absolute error |ei| is smaller than a threshold value eth, the receptor vector xi of the antibody i and the controlling variable σri of immune response of the antibody i will be modified according to the following equation:
| (12) |
| (13) |
where, α and β are the modification coefficients for xi and σri, respectively. The effect of tuning receptor vector xi is decreasing the distance ![]() between the ith antibody and jth antigen and thus increasing their affinity value
between the ith antibody and jth antigen and thus increasing their affinity value ![]() show in Fig. 4. The adjusting of the variable σri results in changing the immune response
show in Fig. 4. The adjusting of the variable σri results in changing the immune response ![]() and consequently decreases its error ei show in Fig. 5.
and consequently decreases its error ei show in Fig. 5.
If error |ei| is larger than the threshold value eth, on the contrary, the components of the affinity matrix Mik will be altered according to the following equations.
Decreasing the affinity mik will cause the reduction of the concentration value of the ith antibody.
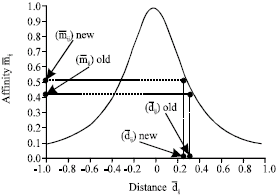 | |
| Fig. 4: | The effect of tuning receptor vector xi (ei>0) |
 | |
| Fig. 5: | The effect of adjusting of the variable σri (ei>0) |
| (14) |
and
| (15) |
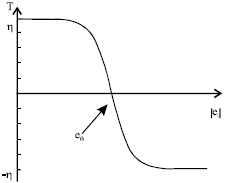
where, η is a adjusting variable show in Fig. 6.
After the tuning procedure, new antibodies should replace the worse antibodies to improve the overall performance of immune network. The ith antibody will be exterminated if its survive probability ρi is smaller than a tolerance valueρtol.
| (16) |
where, N is the total number of antigens utilized in immune network and numi denotes the accumulated count when the ith antibody has the largest concentration value for the jth antigen. Replace these eliminated antibodies with the same number randomly selected from the antigens satisfying largest absolute error (i.e., |ei|.>etol).
Simulation of a 3D parallel robot: The 3D parallel robot shown in Fig. 7 is belonging to the DELTA ROBOT and it is composed of four different parts: the moving platform, the following rods, the actuated arms and the base. The moving platform with three degree of freedom stays constantly parallel to a reference plane and cannot undergo a rotation about the axis perpendicular to this plane. Each actuated arm connects the following rod with a universal joint.
The system consists of four components: user interface, simulation and robot control scheme.
The characteristics of each component are given as follow:
| • | The user interface provides programs with the following functions: generation of the desired reference input; calculation of the feedback information and generation of the commanded input for the x- and y-direction actuator servo systems |
| • | The simulation has two parts: one motion card which includes a programmable the joint angles and joint velocities for the motion of the x- and y-directions; one PCL-816 A/D converter card including two low-pass filter which converts the analog signal from the force sensors to a digital one |
| • | The robot control scheme for maneuvering the handle has the following characteristics: three AC servo motors with screw gears for driving the handle in the x- and y-directions, respectively; one force sensor with two channels: one channel is for the handle force input in the x-direction and the other is for y-direction |
 | |
| Fig. 6: | The adjusting function |
 | |
| Fig. 7: | 3D parallel robot |
In the beginning, we should derive the transfer functions of human arm dynamics. To obtain the dynamics, the operator should hold the handle with zero contact force and follow the motion of the handle until the operator does not follow the handle motion when the input of the handle actuator is with sinusoid signal by increasing frequency from zero. Then, we can obtain the frequency response of the operator dynamics for the x- directions. Moreover, to obtain the transfer function, the following is done: three operators take in turn to grasp the handle. A microcomputer is used to record the input position/output force data. This study utilizes the system identification model of Immune Network to simulate the 3D parallel robot. Additionally, a simple PID controller shown in Fig. 8 is constructed to control the trace of the manipulator.
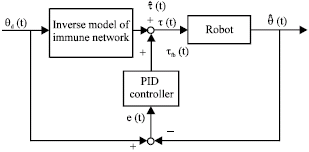 | |
| Fig. 8: | Inverse control diagram using immune network |
 | |
| Fig. 9: | Force eigen-ellipse at z = 450 mm |
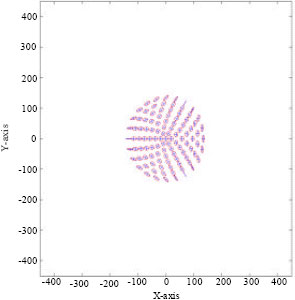 | |
| Fig. 10: | Force eigen-ellipse distribution at z = 650 mm |
The PID controller, a closed-loop control, is used to compensate the trajectory error by inverse model. A general PID controller is considered in this study. The transfer function can be expressed as:
| (17) |
Here, Kp is the proportional constant, Ti is the integral constant and Td is the differential constant. Thus, Eq. 17 can be modified as Eq. 18.
| (18) |
In this study, Kp, Ki and Kd are adjusted by trial-and-error. The simulation results of the trajectory trace control can be expressed as below.
Figure 9 and 10 are force eigen-ellipse distribution plots at x-y planes z = 450 and 650 mm, respectively. We can know the performance characteristics at some point from the shape and size of the eigen-ellipse. The condition when the shape of eigen-ellipse is like a circle indicates that the joint torque and velocity vector norms are equal in any direction. The smaller the area of force eigen-ellipse is, the further the position is from singularity.
This study demonstrates a new method in nonlinear system identification, which a novel nonlinear system NARX model identification scheme based on the immune network is proposed. The immune network can be applied to nonlinear system identification and provided various feasible system models with robust and adaptive characteristics. In this study, a new type of 3D parallel robot arm manipulator with human interface and the parallel motion control of a platform manipulator actuated by three AC servomotors are used to simulate the proposed methodology.
In summary, the results of this study provide effective performance in nonlinear system identification. The immune network which theoretically derived for the application of quantified and graphical performance synthesis is presented. Thus, the capability of this parallel robot in its applications as well as its future research and development are approached. This study combined with the practice and theory, verifying the use of theoretical simulation, so as to facilitate future inferences and follow-up research. The findings of this study should contribute positively to the practice of using immune network to improve the nonlinear system identification and develop a system model with robust and adaptive characteristics.