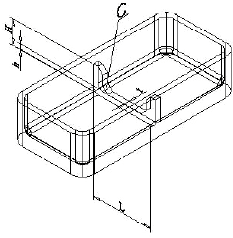
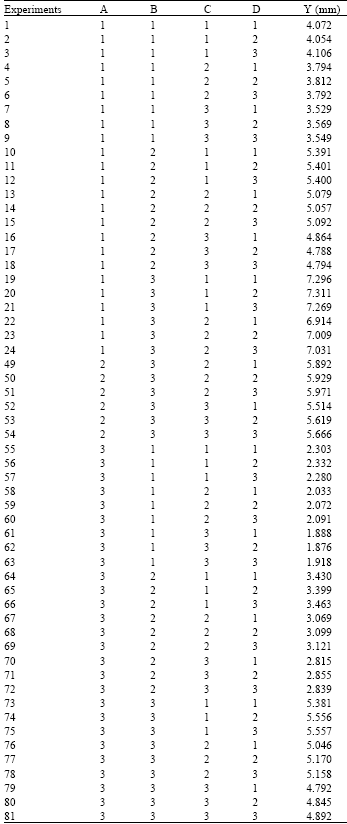
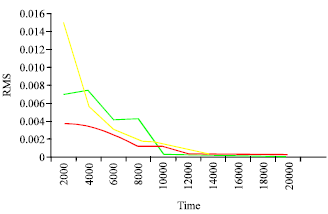
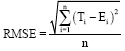Research Article
Quality Prediction Model of Injection-Molded Rib Design using Back-Propagation Network
Department of Information Management, Yu Da College of Business, Miaoli County, Taiwan 361, Repulic of China
Ming-Yung Wang
Department of Mechanical Engineering, Tatung University, Taipei, Taiwan 10451, Repulic of China