Research Article
Neural-Based GA Optimization on Multi-Objective CNC Turning
Department of Information Management, Yu Da College of Business, Miaoli County, Taiwan 361, Republic of China
For metal cutting, the lathe is a common and basic operational process. The controllable parameters of cutting roughly include cutting depth, feed rate, speed and the choices of cutter materials and types. Taguchi design of experiments is an experimental method to efficiently reduce the numbers of conventional experimental tasks, the orthogonal array (Chang, 2000; Wei, 2002) by using design parameter (control factor) in column and standard (level) quantity in row is proposed and further adopted. Nian et al. (1999) used Taguchi method to arrangement experiment for receiving the optimum cutting conditions. Lin et al. (2001) also used convergent network method to construct a surface roughness and cutting force models of lathe cutting. Wang and Huang (2008) used commences by employing an orthogonal array using the Taguchi method to calibrate the factor levels of a heuristic algorithm and to estimate the percent contribution from various individual factors.
Through, the constructed 34 = 81 sets (arranged from L9 (34) orthogonal array (Park et al., 2005) of full experimental (Kan and Chen, 2004; Hong et al., 2002; Moaveni, 2001; Chen and Tsai, 2002), the quality prediction model of multi-objective CNC turning can then be learned and verified by BPN (Back-Propagation Network) (Yang and Lee, 1999; Wang, 2007).
Since, the robust and stochastic search characteristic in GA (Genetic Algorithm), it can locate the global optimal value in a near zone without extra information of derivatives. In this study TOPSIS (technique for order preference by similarity to ideal solution) (Hwang and Yoon, 1981), a multi-objective integration technique, is selected to integrate multiple objectives. Therefore, the BPN is then introduced into GA as the objective function to ultimate the value of TOPSIS by adjusting the control parameters of the CNC turning.
EXPERIMENTAL SETUP
This study is conducted in Yu Da College of Business and as a graduate student’s thesis since September 2007 to July 2008.
The finishing diameter turning operation of S45C (φ45x250 mm) work piece on an ECOCA-3807 CNC lathe is arranged for the experiment. The TOSHIBA WTJNR2020K16 tool holder with MITSUBISHI NX2525 insert is utilized as the cutting tool. The experiment is illustrated as follows. The surface roughness (Ra) of machined work pieces are measured on the MITSUTOYO SURFTEST. The tool wearing length VB2 (mm) (Choudhury and Appa Rao, 1999) in Fig. 1 is scaled on the 3D SONY COLOR VIDEO electronic camera. The tool wearing length is then divided by the volume of material removed as the tool wear ration (mm-2), which is utilized as the indicator of tool wear in this study.
For convenient measurement of cutting force, Fr is divided into three mutual vertical component forces (Fig. 2): tangential force Fz, radial force Fya and axial force FX. Among them, FZ is the greatest which consumes 95% to 99% of machining power (Lin et al., 2001). Therefore, this study focused on the exploration of FZ. In order to establish a cutting force measurement system, a piezoelectric force sensors (KISTLER type 9001 Load Washer) is installed at the bottom of tool base to function as dynamometer (Fuh et al., 1996).
 | |
| Fig. 1: | Tool wear length |
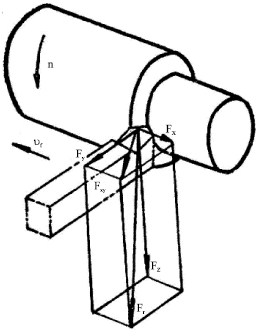 | |
| Fig. 2: | Join force |
The measured lathe cutting signal was amplified by electric charge before sampling and recorded by PC through A/D card (Advantech PCL 816).
METHODS OF RESEARCH
Taguchi method: Taguchi design of experiments is an experimental method in improving the quality characteristic by the appropriate design parameters determined by practical operation on a site or virtual simulation from a computer. To efficiently reduce the numbers of conventional experimental tasks, the orthogonal array (Chang, 2000; Wei, 2002) by using design parameter (control factor) in column and standard (level) quantity in row is proposed and further adopted.
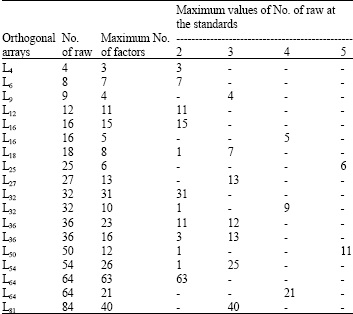
| Table 1: | Standard orthogonal arrays |
 | |
| -: Not available in the tabe | |
By using the analysis of parameters sensitivity to quality characteristic, the optimal parameters can thus be approached by Taguchi method.
The illustration of orthogonal array is usually symbolized as La (bc) wherein L is the symbol of orthogonal array. By using the associated numbers (i.e., a, b, c), both of the format and range can therefore be understood clearly. Here, a representing the total numbers of experiment is demonstrated in the row of the orthogonal table. b, a level number, means that b numbers of design conditions are considered. c, the number of design parameters or factors, is presented in the column of the orthogonal array.
Taguchi robust design method is a powerful tool for the design of a high-quality system (Su, 2002; Palanikumar, 2008). Table 1 includes 18 standard orthogonal arrays listed by Taguchi Method. For direct use of standard orthogonal arrays, the standard number of research-pending factors should be consistent with the standard number of the orthogonal arrays. Meanwhile, we should use the minimum orthogonal array that meets the requirements to save the expenditure of experiments.
In this study, the four turning parameters (cutting depth, feed rate, speed and tool nose runoff) with three different levels (Table 2) are experimentally constructed for the machining operation. In Table 2, the three levels of cutting depth, feed rate and speed are identified from the machining handbook suggested by the tool manufacturer. The tool nose runoff is positioned by using different shims located under the tool holder and determined by measuring the tip after face turned the work piece. When the tool nose is set approximately 0.1 mm higher (lower) than the center of the work piece, it is regard as Level 1 (Level 3).
| Table 2: | Parameters and levels |
 | |
When the tool nose is set within ±0.03 mm, it is considered as Level 2. With the parameters and levels, the 34 = 81 sets of full experimental combinations can then be constructed.
Artificial neural network: Artificial Neural Network (ANN) means the simulation of computation system of biological neural network, including software and hardware and used a great deal of linking artificial neuron to simulate the ability of biological neural network. Artificial neural network is a parallel and distributed computation model that has properties of high parallelism, distributed associative memory, fault tolerance, adaptability and ability to learn from environment. It has been widely used in graphic identification, signal processing, image compression, expert system construction and policy-decision (Wang, 2007).
Based on mentioned above, BPN (Back-Propagation Network) could simply predict external factor and evaluate its value. The structure of BPN can be expressed as shown in Fig. 3. It has excellent learning and prediction ability and can successfully solve many optimization problems. Under the consideration of turning parameters, it should be able to establish a complete prediction model of multi-quality CNC cutting.
According to practical measurement of each quality, the research made up 81 groups of learning examples and made reference to recommending values in selecting 45 groups as training examples. VB.NET language is selected to develop BPN module. Meanwhile, according to related literature, we adopted a hidden layer to learn the experimental results. This study selected cutting depth, feed rate, speed and the tool nose runoff as input layer while multiple qualities were selected as output nodes by output layer. Moreover, the analogy the relationship between input and output through relative small amount experimental data were used to construct multiple quality process predictors and the results of corresponded process by each parameter.
Applying the results of the remaining 36 experiments (81-45 = 36) in the trained pattern with the weight and bias of the trained pattern, the accuracy of multi-quality prediction mechanism of the BPN predictability can then be evaluated and verified through computation of error ratios between the prediction output goals and real output goals.
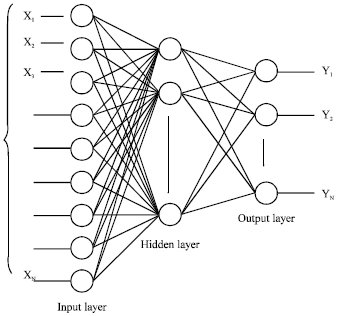 | |
| Fig. 3: | Structure of BPN |
Integration of multiple objectives: Hwang and Yoon (1981) developed TOPSIS (Technique for order preference by Similarity to Ideal Solution) to assess the alternatives before multiple-attribute decision making. TOPSIS considers simultaneously the distance to the ideal solution and negative ideal solution regarding each alternative and also selects the most relative closeness to the ideal solution as the best alternative (Tong et al., 2005).
When the alternative set for multi-attribute decision and evaluation attribute set are described as A = {ai||i - 1, 2…., m} and {g = gi||j = 1, 2…, n} respectively; the computational steps of TOPSIS can be expressed as:
Step 1: This step involves a matrix based on all the information available that describes a material’s attributes and is called a decision matrix. Each row of this matrix is allocated to one alternative and each column to one attribute. The decision matrix can be stated as:
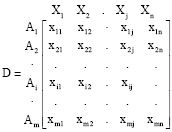 | (1) |
where, Ai represents the possible alternatives, i = 1, 2…., m; Xj denotes the attributes relating to alternative performance, j = 1, 2…., n and xij is the performance of Ai with respect to attribute Xj.
Step 2: Obtain the normalized decision matrix rij. This can be represented as:
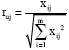 | (2) |
where, rij represents the normalized performance of Ai with respect to attribute Xj.
Step 3: Assume that the weight of each attribute is {wj||j = 1, 2…, n}, the even-weighted normalized decision matrix V = [vij] in this study can be found as:
| (3) |
Where,
Step 4: Develop the ideal (best) and negative ideal (worst) solutions in this step. The ideal and negative ideal solution can be expressed as:
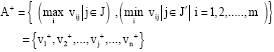 | (4) |
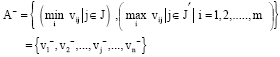 | (5) |
where, J = {j = 1, 2…, n|j} is associated with the beneficial attributes J' = {j = 1, 2…, n|j} is associated with non-beneficial attributes.
Step 5: Determine the distance measures. The separation of each alternative from the ideal one is given by n-dimensional Euclidean distance from the following equations:
| (6) |
| (7) |
Step 6: The proximity of a particular alternative to the ideal solution is expressed in this step as follows:
| (8) |
Step 7: A set of alternatives is made in descending order according to the preference value indicating the most preferred and least preferred feasible solutions.
In this study, the overall relational rating using TOPSIS for multiple precision CNC machining objectives is introduced to the Taguchi experiment as the S/N ratio. Therefore, it is judged as the quality of larger-the-best. In addition to the S/N ratio, a statistical analysis of variance (ANOVA) (Wu and Chyu, 2002) can be employed to indicate the impact of process parameters. In this way, the optimal levels of process parameters can be estimated.
Genetic algorithm: The concept of Genetic Algorithms (GA), first formalized by Holland (1975) and extended to functional optimization by Jong (2000) later involves the use of optimization search strategies patterned after Darwinian notion of natural selection and evolution. During a GA optimization, a set of trial solutions is chosen and evolves toward an optimal solution. In the following we give a short description of the genetic algorithm which is applied as the optimizer in the shape optimization of multi-segments muffler.
| • | Populations and chromosomes: The initial population is built up by randomization. The parameter set is encoded to form a string which represents the chromosome. By evaluation of the object function, each chromosome is assigned with fitness |
| • | Parents: By using the probabilistic computation weighted by the relative fitness, pairs of chromosomes are selected as parents. The weighted roulette wheel selection is then applied. Each individual in the population is assigned space on the roulette wheel which is proportional to the individual relative fitness. Individuals with the largest portion on the wheel have the greatest probability to be selected as parent generation for the next generation. A typical selection scheme, a weighted roulette wheel is depicted in Fig. 4 |
| • | Crossover: Once the mating pool is created, one pair of offspring is generated from the selected parent by crossover. Crossover occurs with a probability of pc. Both the random selection of a crossover and combination of the two parent’s genetic data are then proceeded based on the principle method for the evolution in GA. If the GA decides not to perform crossover, the two selected strings are simply copied to the new population. If crossover does take place, then a random splicing point is chosen in a string, the two strings are spliced and the spliced regions are mixed to create two (potentially) new strings, the child strings. A typical scheme of single-point crossover is depicted in Fig. 5 |
 | |
| Fig. 4: | Weighted roulette wheel method of selection |
 | |
| Fig. 5: | Scheme of single-point crossover |
| • | Mutation: Selection and crossover alone can obviously generate a staggering amount of differing string. However, depending on the initial population chosen, there may not be sufficient variety of strings to assure the GA go through the entire problem space. Some of these problems are overcome by introducing a mutation operator into GA. Genetically, mutation occurs with a probability of pm, which dictates the frequency at which mutation occurs. The mutation probability should be kept very low as a high mutation rate will destroy fit string and degenerate the GA algorithm into a random walk, with all the associated problems. Nevertheless, it does really help to maintain that diversity throughout the Gas iterations. A typical scheme of mutation is depicted in Fig. 6 |
| • | Elitism: To prevent the best gene from the disappearing and improve the accuracy of optimization during reproduction, the elitism scheme to keep best gene in the parent generations is thus presented and developed |
| • | New generation: Reproduction includes selection, crossover, mutation and elitism. The Reduplication continues until a new generation is constructed and the original generation is substituted. Highly fit characteristics produce more copies of themselves in subsequent generation resulting in a movement of the population towards an optimal direction. The process can be terminated when number of generations exceeds a pre-selected value |
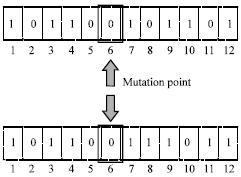 | |
| Fig. 6: | Scheme of mutation |
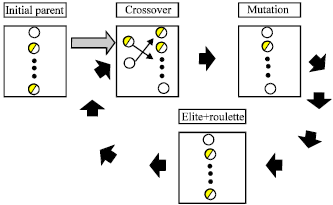 | |
| Fig. 7: | Relationship of GA components |
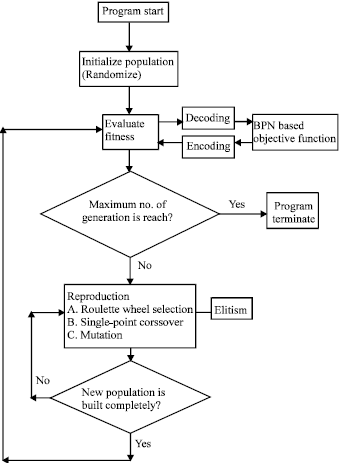 | |
| Fig. 8: | Block diagram of the GA optimization |
The relationship of GA components is shown in Fig. 7. In addition, the block diagram of GA optimization developed for multi-objective CNC machining is depicted in Fig. 8.
This research adopts L9(34) orthogonal array to establish 81 sets of full experiments. This research then adopted Visual Basic program language and MS SQL data to develop multiple quality predictor system. With the randomly selected 45 sets of experimental data, the learning rate as 1 and momentum factor as 0.5; the degree of convergence can be drawn as the error of BPN in Fig. 9 and 10 for Mean Absolute Errors (MAE) and Root Mean Squared Error (RMSE), respectively. It is also found that 4000 times of BPN training through a hidden layer indicated the prediction can reach effective weight and bias.
Through, applying 36 groups to the weight and bias of trained BPN, the verification of BPN can be performed by CPE (cost percentage error) to confirm the accuracy of the BPN predictor. It is found that the prediction. Reached 95.87, 94.32 and 92.29% of accuracy for surface roughness, of tool wear ratio and cutting force, respectively.
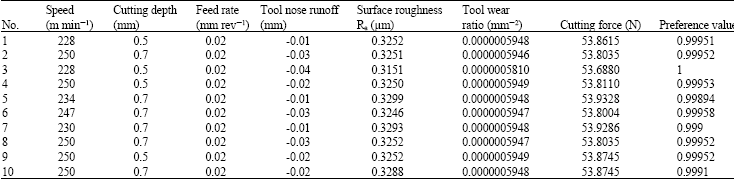
In this study, a novel approach GA based on the principles of natural biological evolution will be used to tackle this optimization of multi-objective CNC turning. To reach the global optimization of multi-objective CNC turning parameters, the trained BPN, TOPSIS algorithm and GA are integrated. In this study, several GA parameters are on trial in various values based on the BPN predictor to find out the optimum GA settings (Table 3). Within the ranges of the CNC turning parameters, the global optimization (Table 4) can be reached after 50000 times of iteration.
It is shown in Table 4 that there exist ten sets of optimum parameter combinations. Through the preference value computed by TOPSIS, it is observer that the third combination has the best preference value. Results show that the GA parameters, including crossover mutation and elitism, are essential in accuracy. Therefore, the multi-objective CNC turning can be globally optimized with surface speed 228 (m min-1), cutting depth 0.5 (mm), feed rate 0.02 (mm rev-1) and tool nose runoff -0.04 (mm).
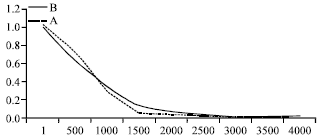 | |
| Fig. 9: | Convergence process of MAE |
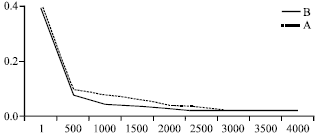 | |
| Fig. 10: | Convergence process of RMSE |
| Table 3: | Optimum GA settings |
| Table 4: | Optimum solutions for multi-objective CNC turning |
 | |
As the CNC (computer numerical controlled) machines play a major role in modern machining industry, the product quality as well as productivity become important issues. The machining process on a CNC (computer numerical controlled) lathe is programmed by speed, feed rate and cutting depth, which are frequently determined based on the job shop experiences. However, the machine performance and the product characteristics are not guaranteed to be acceptable. Therefore, the optimum turning conditions have to be accomplished. The GA optimization on multi-objective CNC turning proposed in this study surely provides an economic and prospective approach than the previous findings (Chudhury and Appa-Rao, 1999; Fuh et al., 1996).
Multi-objective CNC turning parametric optimization is a hard-solving matter because of the interactions between parameters. By following the orthogonal array from Taguchi method, the 81 full experiments can then be set. The BPN is moreover introduced to learn the selected 45 sets of machined results. The remaining 36 sets of machined results are then used to verify and construct a quality predictor of multi-objective CNC turning. It is shown that the prediction accuracy of 95.87, 94.32 and 92.29% for surface roughness, of tool wear ratio and cutting force, respectively.
To achieve the global optimization in GA, several GA parameters are on trial in various values based on the BPN predictor. Results showed that the GA parameters, including crossover mutation and elitism, are essential in accuracy. In this study, a novel approach GA based on the principles of natural biological evolution will be used to tackle this optimization of multi-objective CNC turning.
This study not only proposes a neural-based GA optimization, but also contributes the satisfactory technique for improving the multiple machining performances and finding the global optimum machining parameters in CNC turning with profound insight. Through this study, various multi-objective production optimization can then be achieved in the future study. The competition of manufacturing industry will then be economically excited through the proposed development in this study.
Financial support for this study was provided by the Yu Da College of Business, Miaoli County, Taiwan, Republic of China. The author would also like to thank the anonymous referees who kindly provided the suggestions and comments to improve this work.