Research Article
Formalizing Deniability
School of Computer, South-Center University for Nationalities, Wuhan, 430074, Hubei, Peoples Republic of China
INTRODUCTION
With the development of Internet technology, many transactions are carried out through the Internet. Most of them can not be finished just by face-to-face approach. A key problem of how to authenticate the involved parties’ identities emerges subsequently. Therefore, many authentication protocols have been presented during the past few decades. Authentication protocol based on cryptographic technologies is used to confirm the identities of parties in the communication.
However, some specified Internet applications such as electronic voting and electronic business, require deniable authentication protocols. Deniable authentication protocol allows a sender to authenticate a message for a receiver, in a way that the receiver can not convince a third party that such authentication (or any authentication) ever took place. Deniable authentication protocol has two characteristics that differ from traditional authentication protocol:
| • | Only the intended receiver can authenticate the true source of a given message |
| • | The receiver can not provide the evidences to prove the source of the message to a third party |
The practical secure deniable authentication protocol should have the following properties: completeness or authentication; strong deniability (Raimondo and Gennaro, 2005), weak deniability (Raimondo and Gennaro, 2005), security of forgery attack (Shao, 2004), security of impersonate attack (Shao, 2004), security of compromising session secret attack (Lee et al., 2007), security of man-in-the-middle attack (Han et al., 2005).
These properties play important roles in implementation of secure transactions over the public Internet.
During the past few decades deniable authentication protocol has been studied. Deniable authentication protocol falls into two categories: interactive deniable authentication protocol (Aumann and Rabin, 1998; Dwork et al., 1998; Deng et al., 2001; Fan et al., 2002; Raimondo and Gennaro, 2005; Han et al., 2005; Feng and Ma, 2007) and non-interactive deniable authentication protocol (Shao, 2004; Lu and Cao, 2005a, b; Qian et al., 2005; Shi and Li, 2005; Lee et al., 2007; Meng, 2009b).
Formal method is one important tool to assess deniability of deniable authentication protocol. To our knowledge, the above mentioned deniable authentication protocols were analyzed by informal method. In this study we use the formal method, Kessler and Neumann (1998) logic, to analyze the typical deniable authentication protocols.
The main contributions of this study are summarized as follows:
| • | A formal framework of deniability based on Kessler and Neumann logic is proposed |
| • | Two typical deniable authentication protocols, Fan et al., 2002 interactive deniable authentication protocol and Meng’s non-interactive deniable authentication protocol are analyzed with the informal method and the proposed framework |
In the last several decades a lot of formal methods, for example, communicating sequential processes (Hoare, 1985), BAN logic (Burrows et al., 1989; Boyd and Mao, 1994), strand space (Thayer et al., 1998), spi calculus (Abadi and Gordon, 1997), murφ (Mitchell et al., 1997), Kessler and Neumann logic (Kessler and Neumann (1998)), applied pi calculus (Abadi and Fournet, 2001) have been proposed and applied to analyze key exchange protocols, the complicated electronic voting protocols and electronic commerce protocols (Kailar, 1996; Kremer and Ryan, 2005; Meng et al., 2005; Jonker Hugo et al., 2006; Delaune et al., 2006; Meng, 2007, 2008, 2009a). Kessler and Neumann logic is an important formal method among the above formal methods. Kessler and Neumann logic is a provable sound extension of AUTLOG in order to analyze the most important features of participants in electronic government protocols and electronic commerce protocols. To our knowledge, deniable authentication protocols have not been analyzed by formal method. In this study we use Kessler and Neumann logic to construct a framework for deniability in deniable authentication protocol. The simple and easy to be applied approach focuses on establishing what can construct an evidence of deniability, which can be used to verify deniability and provides a heuristic to take evidence into consideration in the early stages of designing a deniable authentication protocol.
As is often done in protocol analysis, we assume the Dolev-Yao abstraction: cryptographic primitives are assumed to work perfectly, the attacker controls the public channels, at the same time the attacker can see, intercept and insert messages on a public channel, but can only encrypt, decrypt or sign messages for which he has the relevant key.
In this study, we first briefly introduce the Kessler and Neumann logic. Then a framework of strong and weak deniability based on Kessler and Neumann logic is proposed. After that, the framework is applied to analyze the deniability of two typical deniable authentication protocols: Fan et al., 2002 interactive deniable authentication protocol and Meng’s non-interactive deniable authentication protocol. Finally, we conclude the research and suggest feasible future studies.
A BRIEF OVERVIEW OF KESSLER AND NEUMANN LOGIC
Kessler and Neumann logic is a provable sound extension of AUTLOG . The purpose of Kessler and Neumann logic is to analyze the most important features of participants in electronic commerce protocols and electronic government protocols. So, we use the Kessler and Neumann logic to construct the framework of strong deniability and weak deniability in deniable authentication protocol.
Due to space restrictions in the following section we only review the calculus rule, which include inference rule, modalities, possession, recognizability, freshness, oldness, seeing, saying, authentication and key confirmation, comprehension, equivalences, key derivation and provability. Syntax, protocol runs, semantics of the formulae etc. can be found in study (Kessler and Neumann (1998)).
Inference rule
| MP | : | If φ and (φ→ψ) then ψ |
| M | : | If φ is the theorem then P believes φ is a theorem |
Modalities
| K | : | P believes φ ΛP believes (φ→ψ)→P believes ψ |
| 4 | : | P believes φ→P believes¬ P believes φ |
| 5 | : | ¬P believes φ→P believes¬ P believes φ |
Possession
| H1 | : | P sees X →P has X |
| H2 | : | P has X1 ΛP has X2 Λ...ΛP has Xn →ø P has (X1, X2 ... Xn) |
| H3 | : | P has X →P has F (X) |
Recognizability
| R1 | : | P recognizes Xi →P recognizes (X1,...,Xn) |
| R2 | : | P recognizes X ΛP has K-1 →P recognizes enc (K, X) |
| R3 | : | P has X →P recognizes h(X) |
| R4 | : | P has (K+, X) →P recognizes σ(K-1, X) |
Freshness
| F1 | : | Fresh (Xi) →fresh ((X1,...,Xn)) |
| F2 | : | Fresh (X) →fresh (F(X)) |
Oldness
| O1 | : | Old (t,X1,...,Xn) →old (t, Xi) |
| O2 | : | Old (t,F(X)) →old (t, X) |
| O3 | : | Old (t, X) Λt≤t’ →old (t’, X) |
Seeing
| SE1 | : | P sees (X1,...,Xn) →P sees Xi |
| SE2 | : | P sees (X)k ΛP has K-1 →P sees X |
Saying
| NV | : | P said X Λfresh (Xi) →P says X |
| SA1 | : | P said (X1,...,Xn)→P said Xi |
| SA2 | : | P says (X1,...,Xn)→P says Xi |
| SA3 | : | P said h (X) Λ¬ P sees h (X) →P said X |
| SA4 | : | P says h (X) Λ¬ P sees h (X) →P says X |
Authentication and key confirmation:
| A1 | : | Q sees F(K, X) Λ |
| A2 | : | |
| A3 | : |
Comprehension
| C | : | P sees X Λ(XP ≡Y) →P believes P sees Y |
| C1 | : | P recognizes Xi →Λ(X1,...,Xn)P →≡((X))P,..., (Xn)P) |
| C2 | : | P recognizes X ΛP has K¯→(enc(K, X))P ≡(enc (K, XP)) |
| C3 | : | P has X →(h(X))P ≡h(XP) |
| C5 | : | P has ((K+, X)) →(σ(K¯, X))P ≡(σ(K¯, XP)) |
Equivalences
| E1 | : | X ≡Y |
| E2 | : | X ≡Y ΛY ≡Z →X ≡Z |
| E3 | : | X ≡Y →F(X) ≡F(Y) |
| E4 | : | X1 ≡Y1 Λ...ΛXn ≡Yn→(X1,..., Xn) ≡(Y1,..., Yn) |
Key derivation
| S | : |
Provability
 |
FORMALIZING STRONG DENIABILITY AND WEAK DENIABILITY
Formalizing strong deniability: Deniability consists of strong deniability and weak deniability. The purpose of strong deniability is to protect the privacy of receiver. After execution of the deniable authentication protocol the sender can deny to have ever authenticated anything to receiver. If the prover (receiver or the any other party) wants to prove that the sender have authenticated messages to receiver, they must provide all the relevant evidence.
When discussing the strong deniability we always suppose that the sender and the receiver cooperate with the judge or the prover or the any other party, which means that the sender and the receiver provide all the transcripts of the message in the deniable authentication protocol to them.
In order to formally define the strong deniability, we firstly give the formal definition of non-strong-deniability and then we give the formal definition of strong-deniability.
The evidence of non-strong-deniability should include the following information as shown in Fig. 1:
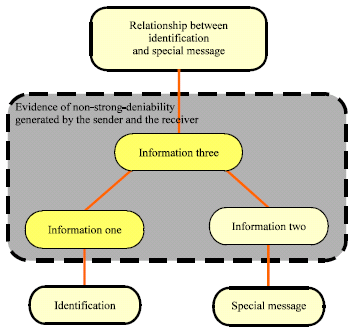 | |
| Fig. 1: | The structure of the evidence of non-strong-deniability |
| • | Information one: The evidence of non-strong-deniability should include the evidence that can prove identification of the sender to the third party, such as the judge and so on |
| • | Information two: The evidence of non-strong-deniability should include the evidence that can prove the sender sends a special message to the receiver |
| • | Information three: the evidence of non-strong-deniability should include the evidence that can prove the sender, not other person or an other third party, authenticate a message |
So, evidence of non-strong-deniability should include Sender_ID (information one), message (information two) and the relationship between Sender_ID (information three). The structure of evidence of non-strong-deniability can be found in Fig. 1.
Formal definition of strong deniability: If a deniable authentication protocol satisfies the following conditions at the same time, we argue that the deniable authentication protocol has non-strong-deniability, otherwise has strong deniability.
Condition one: {Prover believes prover {Authority said Sender _ID} to J until t}.
Condition one shows that prover has sender’s legal identification, Sender_ID, that is issued by the legal authority, not by other illegal party.
Condition two: {Prover believes prover canprove {sender said Message} to J until t}.
Condition two shows that the prover confirms that the sender sends a message to receiver.
Condition three:
 |
Condition three shows that the sender who has the Sender_ID, not other sender with Sender_ID sends a special message, or the sender who has the Sender_ID sends other message.
Proving rule P7:
 |
The P7 rule shows that if the prover confirmed that the sender’s identity Sender_ID and can get a message and can prove that the message is generated by the sender who has the legal identification Sender_ID, he can prove sender said or can generate the evidence of non-strong-deniability, which means that the deniable authentication protocol has the non-strong-deniability, otherwise has strong deniability.
Formalizing weak deniability: The purpose of weak deniability is to protect the privacy of sender. After execution of the deniable authentication protocol the receiver can prove to have spoken to the sender but not the content of what the sender authenticated in a way that the receiver can not convince a third party that such authentication. If the receiver want to prove that the sender have authenticated messages to receiver, he must provide the evidence related to the thing.
When discussing the weak deniability we always suppose that only the receiver generates the evidence that the sender have authenticated messages to receiver. The receiver can not get the secret information of the sender, for example the private key of the sender.
The idea of formalizing weak deniability is similar to the idea of formalizing strong deniability. We firstly give the formal definition of non-weak-deniability and then the formal definition of weak deniability is proposed.
The evidence of non-weak-deniability should include the following information:
| • | Information one: The evidence of non-weak-deniability should include the evidence that can be used to prove identification of the sender to the third party, such as the judge and so on |
| • | Information two: The evidence of non-weak-deniability should include the evidence that can prove the sender sends a special message to the receiver |
| • | Information three: The evidence of non-weak-deniability should include the evidence that can prove the sender, not other person or third party, authenticate a special message |
So, evidence of non-weak-deniability should include Sender_ID (information one), Message (Information two) and the relationship between Sender_ID (information three). The structure of evidence of non-weak-deniability can be found in Fig. 2.
In the following section we give the formal definition of non-weak-deniability based on Kessler and Neumann logic.
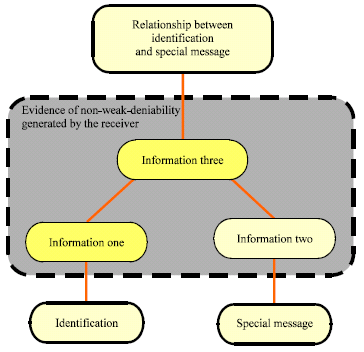 | |
| Fig. 2: | The structure of the evidence of non-weak-deniability |
Formal definition of weak deniability: If a deniable authentication protocol satisfies the following conditions at the same time, we argue that the deniable authentication protocol has not weak deniability, otherwise has weak deniability.
Condition one: {Receiver beleives receiver canprove {Authority said Sender_ID} to J until t.
Condition one shows that receiver has sender’s legal identification, Sender_ID, that is issued by the legal authority, not by other illegal party.
Condition two: {Receiver beleives receiver canprove {Authority said Sender_ID} to J until t}.
Condition two shows that the prover confirmed that the sender sends a special message.
Condition three:
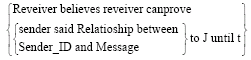 |
Condition three shows that the sender who has the Sender_ID not other sender with Sender_ID, sends a special message, or the sender who has the Sender_ID sends other message.
Proving rule P8:
 |
The P8 rule shows that if the receiver confirms that the sender’s identification Sender_ID, can get a special message and can prove the special message is generated by the sender who has the legal identification Sender_ID, he can generate the evidence of non-weak-deniability, which means that the deniable authentication protocol has non-weak-deniability, otherwise has weak deniability.
APPLICATIONS ON DENIABLE AUTHENTICATION PROTOCOLS
Here, we give two examples of applications on the deniable authentication protocols. One is application on Fan et al., 2002 protocol, which is a typical interactive deniable authentication protocol. The other example is application on Meng protocol, which is the typical non-interactive deniable authentication protocol.
Application on Fan et al., 2002 protocol: Fan et al., 2002 deniable authentication protocol, which is based on the Deffie-Hellman key agreement protocol, has weak deniability and resist person-in-the-middle attack used the digital certificate issued by the certification authority. Firstly, we give an informal description, which is base for the formal analysis that follows. Then we analyze strong deniability and weak deniability with the framework proposed by us. At last we point that Fan et al., 2002 protocol has weak deniability and has not strong deniability.
A brief overview of Fan et al., 2002 protocol: Fan et al., 2002 deniable authenticate protocol have three participants: a sender, a receiver and an inquisitor INQ. INQ sits on the link between the sender and the receiver and can monitor the information between the sender and the receiver and injects a message of his own. INQ can later force the sender and the receiver to reveal all the security data when we formally analyze the strong deniability. PD is the public directory.
The sender has a digital certificate issued by CA. The digital certificate contains the public key SPU of the sender and the signature of CA for this certificate. The receiver can obtain the public key CAPU of CA and verify it. The private key SPR of the sender is kept secret. The sender and the receiver will use two public prime numbers g and n, as does the original Deffie-Hellman protocol. A collision-free hash function is required. Figure 3 describes Fan et al., 2002 deniable authentication protocol.
The process of Fan et al. protocol is as follows:
| • | The sender chooses a random large integer x and computes: X = gx mod n X’ = ESPR and then sends X’ to the receiver |
| • | The receiver chooses a random large integer y and sends the sender: Y = gy mod n |
| • | The receiver decrypts X’ and gets X = ESPU (X’) and then the receiver computes k = XY mod n |
| • | The sender computes k’ = YX mod n, we can find k’ = YX mod n = k = XY mod n, so, the sender and receiver share a same session key k |
| • | If the sender wants to send a message M to the receiver, he will send M||D = H(k,M) |
| • | The receiver computes D’ = H(k’, M). If D’ = D, the receiver accepts M otherwise rejects it |
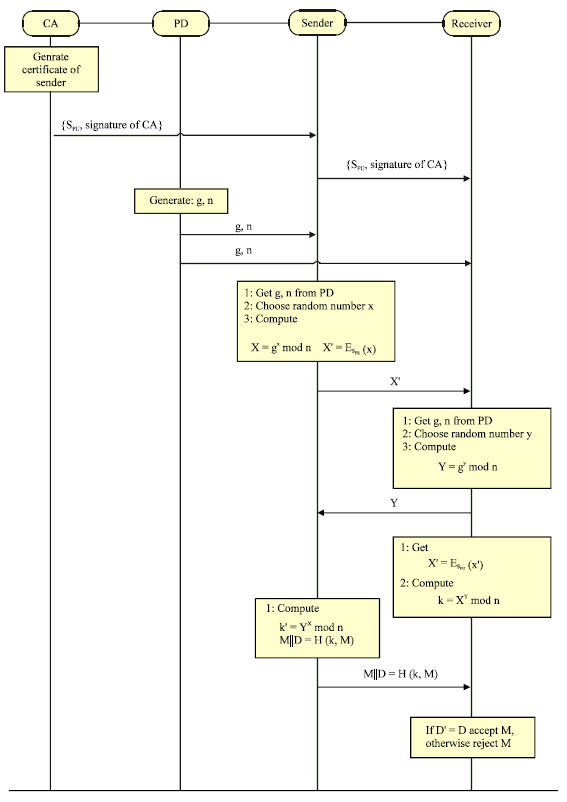 | |
| Fig. 3: | Fan et al., 2002 deniable authentication protocol |
Informal proof of deniability in Fan et al., 2002 protocol:
Here, we give the informal proof of strong deniability and weak deniability.
Strong deniability: After the execution of the protocol the sender can deny to have ever authenticated anything to receiver.
Informal proof: The sender and the receiver cooperated with the judge. The sender’s certificate, which includes the public key SPU of the sender in CA, is available by anyone. So, the receiver and the judge can get the public key certificate of sender. According to the protocol in order to prove that M||D = H(k,H) is sent by the sender, the judge must force the sender to provide his public/private key and the transcript of X = ESPR, (X’), M||D = H (k, M) and k’ = YX mod n. At the same time, the receiver can provide the transcript of k = XY mod n. So, the judge assures that the sender can not deny to have ever authenticated M to receiver. Hence, Fan et al., 2002 protocol is not strong deniability.
Weak deniability: The deniable authentication protocol is weak deniability. The receiver can prove to have spoken to the sender but not the content of what the sender authenticated in a way that the receiver can not convince a third party that such authentication.
Informal proof: The sender can not cooperate with the receiver and the judge. In other words, the sender can not provide his private key and transcripts of X = gx mod n and X’ = ESPR (X) to the receiver and third party. After sharing a key with the sender, the receiver can generate a message M’, which is different from M. The receiver can compute D’ = H(k’, M’) (D’, M’) is different from the actual message generated by the sender, so the receiver can simulate the authenticated message of the sender. Hence, the third party can not assure that M’ is sent by the sender. So, Fan et al., 2002 protocol is weak deniability.
Formal proof of deniability in Fan et al., 2002 protocol:Here, we give the formal proof of strong deniability and weak deniability.
Formal proof of strong deniability in Fan et al., 2002 protocol: Here, we give formal proof of strong deniability. Present idea is that we prove that prover can generate the evidence of non-strong-deniability, which means that Fan et al., 2002 protocol is not strong deniability.
In order to proving that Fan et al., 2002 protocol is not strong deniability we need to prove that the following result:
 |
Then we can apply the proving rule P7 and get:
Present goal:
If we can get:
 |
We can get:
So, Fan et al., 2002 protocol is not strong deniability.
Beginning the proof: When we discuss the strong deniability we always suppose that the sender and the receiver cooperate with the judge or the prover, which means that the sender and the receiver provide all the transcripts of the message in the deniable authentication protocol.
So, after an execution of the Fan et al., 2002 protocol, prover can get:
 |
From the sender and the receiver.
Prerequisites
| M1 | : | Prover has known the sender’s public and private keys |
| M2 | : | All participants trust into the certification authority and believe that especially the judge shares this trust |
| M3 | : | The certificates are completely understood by everyone |
| M4 | : | Prover can comprehend (k, M) and prover believes J comprehends (k, M) as well |
 |
Neither prover nor J need to understand the hash value HASH (k, M).We only assume that prover believes:
((HASH (k, M))prover)J ≡(HASH (k, M))prover |
| M5 | : | Prover believes that no person signs forwarded messages that he does not understand. In addition prover believes that J shares his belief |
Verification: After the execution of Fan et al., 2002 protocol, prover can get:
 |
From the sender and the receiver. We use the notations of Kessler and Neumann logic to describe the message.
Som we have:
 | (1) |
| | (2) |
| | (3) |
| | (4) |
| | (5) |
| | (6) |
| | (7) |
| | (8) |
 | (9) |
 | (10) |
| | (11) |
| | (12) |
| | (13) |
 | (14) |
| | (15) |
 | (16) |
 | (17) |
 | (18) |
| | (19) |
| | (20) |
| | (21) |
| | (22) |
 | (24) |
| | (25) |
| | (26) |
| | (27) |
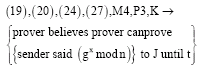 | (28) |
| | (29) |
| | (30) |
| | (31) |
| | (32) |
| | (33) |
| | (34) |
| | (35) |
According to Fan et al., 2002 protocol and Eq. 15 and 32, we can get condition three:
 | (36) |
Applying proving rule 7:
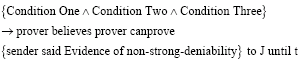 |
We can get:
So, we can get the conclusion: Fan et al. (202) deniable authentication protocol is not strong deniability.
End of the proof: This conclusion is the same to the previous informal proof.
Formal proof of weak deniability in Fan et al., 2002 protocol: The proof of weak deniability is similar to the proof of strong deniability.
The idea is that we prove that receiver can not generate the evidences of non-weak-deniability, which means that Fan et al., 2002 protocol is weak deniability.
In order to proving that Fan et al., 2002 protocol is weak deniability we need to prove that we can not get the following result:
 |
Then we can not apply the proving rule P8:
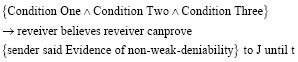 |
and get:
Present goal:
 |
So, Fan et al., 2002 protocol is weak deniability.
Beginning the proof: When we discuss the weak deniability we always suppose that only the receiver generates the evidence that the sender have authenticated messages to receiver. The receiver can not get the secret information of the sender, for example the private key of the sender:
So, after an execution of the Fan et al., 2002 protocol, the receiver can get:
from himself.
Prerequisites
| M1 | : | Receiver has known the sender’s public key |
| M2 | : | All participants trust into the certification authority and believe that especially the judge shares this trust |
| M3 | : | The certificates are completely understood by everyone |
| M4 | : | Receiver can comprehend (k, M) and receiver believes J comprehends (k, M) as well |
 |
Neither receiver nor J need to understand the hash value HASH (k, M).We only assume that receiver believes:
| M5 | : | Receiver believes that no person signs forwarded messages that he does not understand. In addition receiver believes that J shares his belief |
Verification: After the execution of Fan et al., 2002 protocol, receiver can get message:
 |
from himself. We use the notations of Kessler and Neumann logic to describe the message.
The complicated procedure is similar to the proof procedure of non-strong-deniability. Here, we only give the results.
Owning to certificate of the sender, the third party can verify the sender’s identification.
So, we have:
Condition one:
According to Fan et al., 2002 protocol the receiver can not get the sender’s private key and transcripts of X = gx mod n and X’ = ESPR (X). After sharing a key with the sender, the receiver can generate a message M’, which is different from M. The receiver can compute D’ = H (k’, M’) (D’, M’) is different from the actual message generated by the sender, so, the receiver can simulate the authenticated message of the sender. Hence, the third party can not assure that M’ is sent by the sender.
We can not get:
Condition two:
Condition three:
 |
According to the proving rule P8, Fan et al., 2002 protocol has non-weak-deniability. In other words Fan et al., 2002 protocol has weak deniability.
End of the proof: This conclusion is the same to the previous informal proof.
APPLICATION ON MENG PROTOCOL
Here, firstly, we give a brief overview of Meng deniable authentication protocol (Meng, 2009b). Then we give an informal description that is used as a basis for a formal description that follows. we analyze deniability with the framework proposed by us. At last we point that the protocol is strong and weak deniability.
A brief overview of Meng protocol: Meng protocol (Meng, 2009b) is a secure non-interactive deniable authentication protocol based on discrete logarithm problem. Meng protocol consists of authority, the sender and the receiver. Meng protocol is secure and has properties: completeness, strong deniability, weak deniability, security of forgery attack, security of impersonate attack, security of compromising session secret attack and security of man-in-the-middle attack.
In Meng protocol the author assumes that the attacker can not monitor the communication between the sender and receiver during the execution of run (Fig. 4).
Meng protocol is described as the following:
Initialized phrase: The authority performs the following steps:
| • | Firstly, choose a large prime numbers p; secondly, compute a random multiplicative generator element g in finite field of p elements: GF (p); thirdly, send the g, p to the bullet board |
The sender performs the following steps:
| • | Firstly, pick a serial random numbers ri ε Uzp-1 |
The receiver performs the following steps:
| • | Firstly, pick a random number x ε Uzp-1 RPR = x; secondly, compute his public key by: RPU = gx (mod p); thirdly, send the RPU to the bullet board |
| • | When finishing the initialized phrase the sender has serial public and private keys |
Execution of protocol phrase: The sender:
| • | Firstly, chooses randomly a public and private key |
| • | Secondly, computes: δ = hash (m) |
| • | Thirdly, sends |
The receiver:
Firstly, compute ![]()
Secondly, verifies
if the result is true, the receiver accepts it. Otherwise the receiver rejects it
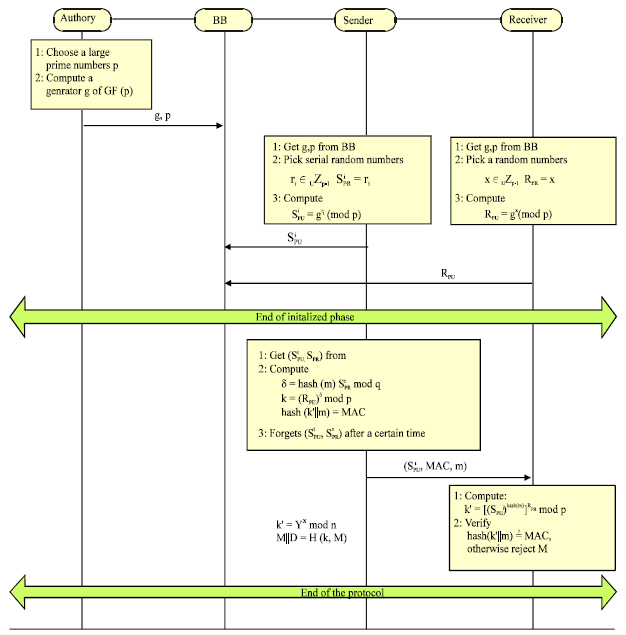 | |
| Fig. 4: | Meng deniable authentication protocol |
Informal proof of deniability in Meng protocol: Here, we give the informal proof of strong deniability and weak deniability.
Strong deniability: After the execution of the protocol the sender can deny to have ever authenticated anything to receiver.
Informal proof: The sender and the receiver cooperated with the judge. The sender’s public key ![]() on the bullet board is available at the time of execution of the protocol by anyone. So the receiver can get the public key of sender. After the execution of the protocol the sender forgets his public and private key
on the bullet board is available at the time of execution of the protocol by anyone. So the receiver can get the public key of sender. After the execution of the protocol the sender forgets his public and private key ![]() According to the protocol in order to prove that
According to the protocol in order to prove that ![]() is sent by the sender, the judge must force the sender to provide the transcript of
is sent by the sender, the judge must force the sender to provide the transcript of ![]() Because the sender forgets his public and private key
Because the sender forgets his public and private key ![]() he can not provide the transcript of:
he can not provide the transcript of:
So, the sender can deny to have ever authenticated anything to receiver.
Weak deniability: The deniable authentication protocol is deniable. The receiver can prove to have spoken to the sender but not the content of what the sender authenticated in a way that the receiver can’t convince a third party that such authentication.
Informal proof: The sender can not cooperate with the receiver and the judge. After receiving ![]() the receiver can authenticate the source of the message m which being sent by the sender with his private key SPR. But the receiver can not prove the source of m to a third party for the following reasons.
the receiver can authenticate the source of the message m which being sent by the sender with his private key SPR. But the receiver can not prove the source of m to a third party for the following reasons.
According to the protocol the receiver has the ability to generate many fake messages ![]() which can be authenticate with the equation
which can be authenticate with the equation ![]() and m’ because the receiver knows his private key RPR. The third party can verify the fake
and m’ because the receiver knows his private key RPR. The third party can verify the fake ![]() with the k’ and m’ according to the protocol. So, the third party can not assure that m’ is sent by the sender. Hence the proposed protocol has weak deniability.
with the k’ and m’ according to the protocol. So, the third party can not assure that m’ is sent by the sender. Hence the proposed protocol has weak deniability.
Formal proof of deniability in Meng protocol: Here, we give the formal proof of strong deniability and weak deniability in Meng protocol.
Formal proof of strong deniability in Meng protocol: The proof of strong deniability in Meng protocol is similar to the proof of strong deniability in Fan et al., 2002 protocol.
The idea is that if prover can not generate the evidence of non-strong-deniability, Meng protocol is strong deniability.
In order to proving that Meng protocol is strong deniability we need to prove that we can not get the following result:
 |
Then we can not apply the proving rule P7 and can not get:
Present goal:
or
So, Meng protocol is strong deniability.
Beginning the proof: When discussing the strong deniability we always assume that the sender and the receiver cooperated with the judge or prover. The prover can get the secret information of the sender, for example the private key of the sender. According to Meng protocol after a certain time of an execution of Meng protocol, the sender forgets his public/private keys ![]() the prover can not get
the prover can not get ![]()
So, after an execution of Meng protocol in a long time, prover can get:
from the sender and the receiver.
Prerequisites
| M1 | : | Prover has known the receiver’s public and private keys |
| M2 | : | All participants trust into the BB and believe that especially the judge shares this trust |
| M3 | : | The public keys are completely understood by everyone |
| M4 | : | Prover can comprehend m and prover believes J comprehends m as well |
Neither receiver nor J need to understand the hash value HASH (k,M). We only assume that receiver believes:
| M5 | : | Receiver believes that no person signs forwarded messages that he does not understand. In addition receiver believes that J shares his belief |
Verification: After the execution of Meng protocol, receiver can get:
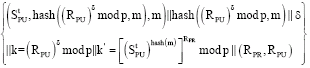 |
from the sender and the receiver. We use the notations of Kessler and Neumann logic to describe the message.
The complicated procedure is similar to the proof procedure of non-strong-deniability in Fan et al., 2002 protocol. Here we only give the results.
Due to that we do not use the certificate in Meng protocol; prover can not verify the sender’s identification. So, we have not:
Condition one:
According to Meng protocol prover can not get the sender’s private key and transcripts of ![]() In order to prove that
In order to prove that ![]() is sent by the sender, prover must force the sender to provide the transcript of
is sent by the sender, prover must force the sender to provide the transcript of ![]() Because the sender forgets his public/private keys
Because the sender forgets his public/private keys ![]() he can not provide the transcript of
he can not provide the transcript of
So, the sender can deny to have ever authenticated anything to receiver. We can not get:
Condition two:
Condition three:
 |
We can not apply Proving rule P7 and can not get:
Hence, Meng protocol has strong deniability.
End the proof
This conclusion is the same to the previous informal proof.
Formal proof of weak deniability in Meng protocol: The proof of weak deniability is similar to the proof of strong deniability.
The idea is that we prove that receiver can not generate the evidence of non-weak-deniability, which means that Meng protocol is weak deniability.
In order to proving that Meng protocol is weak deniability we need to prove that we can not get the following result:
 |
Then we can not apply the Proving rule P8 and can not get:
Present goal:
or
or
 |
We can not get:
So, Meng protocol is weak deniability.
Beginning the proof: When we discuss the weak deniability we always suppose that only the receiver generates the evidence that the sender have authenticated messages to receiver. The sender does not cooperate with the receiver and the judge. The sender’s public key ![]() on the bullet board is available at the time of execution of the protocol by anyone. So the receiver can get the public key of sender.
on the bullet board is available at the time of execution of the protocol by anyone. So the receiver can get the public key of sender.
After an execution of Meng protocol in a short time, the receiver can get:
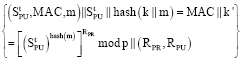 |
Prerequisites
| M1 | : | Receiver has known the sender’s public key |
| M2 | : | All participants trust into the BB and believe that especially the judge shares this trust |
| M3 | : | The public keys are completely understood by everyone |
| M4 | : | Receiver can comprehend m and receiver believes J comprehends m as well |
Neither receiver nor J need to understand the hash value HASH(k,M). We only assume that receiver believes:
| M5 | : | Receiver believes that no person signs forwarded messages that he does not understand. In addition receiver believes that J shares his belief |
Verification: After the execution of Meng protocol in a short time, receiver can get:
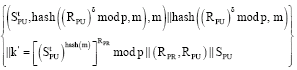 |
We use the notations of Kessler and Neumann logic to describe the message.
The complicated procedure is similar to the proof procedure of non-strong-deniability. Here, we only give the results.
Due to the public key of the sender in BB in a short time, the receiver can verify the sender’s identification in a short while.
So, we have:
Condition one:
According to Meng protocol the receiver can not get the sender’s private key and transcripts of
After receiving ![]() the receiver can authenticate the source of the message m which being sent by the sender with his private key SPR.
the receiver can authenticate the source of the message m which being sent by the sender with his private key SPR.
Due to the ability to generate many fake messages ![]() which can be authenticate with the equation
which can be authenticate with the equation ![]() mod p and m’ with the receiver’s private key RPR, the third party can verify the fake
mod p and m’ with the receiver’s private key RPR, the third party can verify the fake ![]() with the k’ and m’ according to the protocol. So, the third party can not assure that m’ is sent by the sender without the sender’s identification. Hence, we can not get:
with the k’ and m’ according to the protocol. So, the third party can not assure that m’ is sent by the sender without the sender’s identification. Hence, we can not get:
Condition two:
Condition three:
 |
So, we can not get:
|
This conclusion is the same to the previous informal proof.
In the past, as an important tool, many formal methods proposed are used to assess security protocols, except the deniable authentication protocol to our knowledge.
In this study, we formally assess the deniability by proposing a formal framework based on Kessler and Neumann logic, which can be found in Table 1 and 2. The simple and easy to be generalized approach focuses on establishing what can construct an evidence of deniability, which makes it possible to verify deniability and provides a heuristic to take evidence of deniability into consideration in the early stages of designing a deniable authentication protocol .
Then, the framework is applied to analyze deniability of two typical deniable authentication protocols. We found that Fan et al., 2002 protocol has weak deniability but not strong deniability and Meng protocol has both strong and weak deniability. The result is consistent with that of informal method. Details of the formal result can be found in Table 3 and 4, respectively.
| Table 1: | The notations definition of deniability |
 | |
| Table 2: | Formal definition of deniability and non-deniability |
 | |
| The mark ©I represents the protocol has the property. The mark | |
| Table 3: | The result of proof of Fan et al., 2002 protocol |
 | |
| The mark ©I represents the protocol has the property. The mark | |
| Table 4: | The result of proof of Meng protocol |
 | |
| The mark ©I represents the protocol has the property. The mark | |
Further studies concentrate on formal analysis of the security of forgery attack, security of impersonate attack, security of compromising session secret attack, security of man-in-the-middle attack.