ABSTRACT
In this study, a novel energy-balancing unequal clustering protocol (EB-UCP) for wireless sensor networks is presented. EB-UCP achieves a good performance in terms of lifetime by unequal clustering and balancing the energy load among all the nodes. An unequal clustering algorithm from probability view is employed to form clusters. Clusters closer to the sink node have smaller sizes than those farther away from the sink node, thus cluster heads closer to the sink node can preserve more energy for the purpose of inter-cluster data forwarding. In addition, the distribution of sensor nodes is deployed according to the energy-balancing layered algorithm and therefore the energy consumption in every layer is nearly equal. Finally, an energy-efficient data transmission mechanism on basis of the above is proposed. Simulation studies show that EB-UCP leads to more uniform energy dissipation and enlarges the lifetime of networks than EEUC (Energy Efficient Unequal Clustering) and LEACH (Low-Energy Adaptive Clustering Hierarchy).
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/itj.2009.57.63
URL: https://scialert.net/abstract/?doi=itj.2009.57.63
INTRODUCTION
Recent advances in wireless communication and electronics have enabled the development of low-cost, low-power, multi-functional sensors that are small in size and able to communicate untethered within a short distance. In order to achieve energy efficiency and increase network scalability, sensor nodes can be organized into clusters. Communication within a cluster as well as communication between different clusters can be organized as a combination of one-hop and multi-hop communication. In one-hop communication, every sensor node can directly reach the sink node, while in multi-hop communication, nodes have limited transmission range and therefore are forced to route their data over several hops until the data reach the sink node. In both models, there is an unavoidable problem of unbalanced energy dissipation among different nodes, leading to the situation where some nodes lose energy at a higher rate and die much faster than others, possibly reducing sensing coverage and leading to network partitioning. For single-hop communication, the nodes furthest away from the sink node are the most critical nodes, while in multi-hop communication, the nodes closets to the sink node are burdened with a heavy relay traffic load and die first, i.e., the hot spot problem (Perillo et al., 2005).
LEACH (Heinzelman et al., 2002) is a well-known hierarchical architecture routing algorithm, which uses randomization to rotate the Cluster Heads (CHs) and achieves significant improvement compared to direct approach. However, this approach allows only one-hop clusters to be formed and the hot spot problem does not be considered. Li and Mohapatra (2005) presented a mathematical model to analyze hot spot problem and characterize energy hole problem in Wireless Sensor Networks (WSNs). Based on a traffic perspective, this analytical model examines the validity of several possible schemes aiming to mitigate or solve the energy hole problem. It is observed that in a uniformly distributed sensor networks, clustering deployment and data compression have a positive effect. Olariu and Stojmenovic (2006) presented the first theoretical work to analyze avoidance of the energy hole problem and it has been proven that the unbalanced energy depletion is intrinsic and no routing strategy can avoid under some specific conditions in this study. Perillo et al. (2004) formulated the transmission range distribution optimization problem and derived a linear programming model to obtain the maximizing WSNs lifetime. EEUC (Li et al., 2005) use the competition radius to produce the unequal clustering, but this mechanism does not consider density of sensors deployed that might cause much workload on CHs and too much communication overhead. Soro and Heinzelman (2005) proposed an unequal clustering size mode for network organization. However, it shows somewhat an unrealistic architecture since they assume that CHs with super power are deployed or move to the best position where minimizes energy consumption. It also considers only 2 layers, which means scalability is not in concern.
In this study, a novel Energy-Balancing Unequal Clustering Protocol (EB-UCP) for WSNs is proposed. In EB-UCP, the entire network has been divided into some layers and clusters from probability view. The number of clusters closer to the sink node is bigger than those farther away from sink node. However, the number of nodes in each cluster closer to the sink node is smaller than those farther away from sink node. Thus inner CHs can reduce the energy consumption within a cluster and preserve more energy for inter-cluster data relaying. In order to balance the energy dissipation in every layer, the reasonable ratios of distribution density among layers are derived according to energy-balancing principle. Therefore, the energy consumption in every layer is nearly equal after such a deployment and the hot spot problem can be effectively mitigated by this way. Finally, an energy-efficient data transmission mechanism is presented on basis of unequal clustering algorithm and energy-balancing layered algorithm. Theoretical analysis and simulation studies show that EB-UCP outperforms in terms of balancing energy dissipation among sensor nodes and enlarging the lifetime of networks than EEUC and LEACH.
EB-UCP: AN ENERGY-BALANCING UNEQUAL CLUSTERING PROTOCOL
Network model: All the nodes are assumed to be deployed in a circular area with a radius of R. The only sink is located at the center of the area. This represents a layered network where every layer contains a particular number of clusters, as shown in Fig. 1.
All the sensor nodes are homogeneous and have an ID number and the i-th corona is denoted by layer Li. The maximum layer number is k and the width of each layer is r. For sake of simplicity, each sensor node is assumed to generate and send h bits of data per unit time. Nodes belonging to layer {Li|i≠ k} will forward both the data generated by them and the data generated by nodes from layers {Lj|(i+1)≤j≤k}. The nodes in the outermost, Lk, need not forward any data. The model for energy dissipation is taken from LEACH, where, for our multi-hop forwarding scheme we assume a free space propagation channel model. The energy spent for transmission of a h-bit packet over distance d is:
 | |
| Fig. 1: | A circular area consisting of coronas |
Etx (h, d) = h(e1+e2d2) | (1) |
And the energy spent on receiving a h-bit packet is:
Erx (h, d) = he1 | (2) |
The electronics energy, e1, depends on factors such as the digital coding, modulation, filtering and spreading of the signal. The amplifier energy, e2, depends on the distance to the receiver and the acceptable bit-error rate.
Unequal clustering algorithm: At network deployment stage, sink node broadcasts a hello message to all sensor nodes. Through the Received Signal Strength Indication (RSSI), each node can compute the approximate distance to the sink and the layer number of node belonging according to algorithm which is proposed by De et al. (2006). After the computation, each sensor sends its corresponding level number to the sink node. The sink knows the maximum layer number k and broadcasts it to all sensor nodes.
The key idea of clustering algorithm is to utilize clusters of unequal sizes to mitigate the hot spot problem. Layers are assigned different probabilities according to the distance from sink node and the layers closer to the sink node have greater probabilities than those farther away from sink node. Low probability indicates small number of CHs, which also means that each CH will occupy a huge cluster area with probably many non-CH nodes. Therefore, it is fair that closer sensor nodes get higher probability to be chosen as CHs in the perspective of balanced energy dissipation through the whole network. In order to balance energy depletion among nodes, the CH selection in every layer is primarily based on the residual energy of tentative cluster heads. The node i’s probability of becoming a CH pi will be computed as follows:
(3) |
where, pmax is the node’s probability of becoming a CH in first layer, pmin is the node’s probability in the kth layer, j represents node i’s layer number.
In our algorithm, let pmax = 1, That is, nodes in first layer all become CHs as they have direct transmission to sink node with small amount of energy and fully devote to heavy relaying traffic. The pseudocode for an arbitrary node i at the cluster head selecting stage is given in Fig. 2.
Each node in every layer become a tentative CH with the same probability pi which is defined by Eq. 3. Other nodes keep sleeping until the CH selection stage ends. Each tentative CH maintains a set SCH of its adjacent tentative CHs. Tentative head q is an adjacent node i if q is in i’s intra-cluster transmission range and two nodes are in the same layer. In lines 4-5 of Fig. 2, each tentative CH broadcast a CompeteCH_msg which contains its id, layer_id and residual energy. After the construction of SCH has been finished in lines 7-8, each tentative CH checks its SCH and makes a decision whether it can become a CH in lines 9-19. Before deciding what its role is going to be, i needs to know what each node q in its SCH such that q.Ecurrent>i.Ecurrent has decided for itself. In lines 10-12, once node i finds that its residual energy is more than all the nodes in its SCH, it will win the competition and broadcast a FinalCH_msg to inform its adjacent tentative CHs. In lines 13-15, if qis in i’s SCH and i receives a FinalCH_msg from q, i will give up the competition immediately and inform all nodes in its SCH by broadcast a QuitEle_msg. In lines 16-19, if i receives a QuitEle_msg from q and q belongs to i.SCH, i will remove q from its SCH.
 | |
| Fig. 2: | Cluster head competitive algorithm |
After CHs have been selected, each CH broadcasts a CH_ADV_msg across the network field. Each ordinary node chooses its closest CH with the largest received signal strength and then informs the CH by sending a JOIN_CLUSTER_msg.
Energy-balancing layered algorithm: The energy balancing in every layer is considered in this subsection. In order to measure the data aggregation by CH within a cluster, all CHs are assumed to equally compress the data, where this efficiency is expressed by the aggregation coefficient α and energy dissipation for unit data aggregation is e3. If let Ni and ρ1 denote the number and distribution density of layer Li, respectively. The total energy consumption in each layer can be calculated. According to the above assumptions and network model, the outermost layer Lk only needs to forward data generated by themselves. Thus energy dissipation per unit time of each CH in outermost layer Lk is:
(4) |
Equation 4 shows that the smaller α is, the higher efficiency of data aggregation by CH is. The energy dissipation per unit time of each non-CH in outermost layer Lk is:
(5) |
Thus, the energy consumption per unit time of all nodes in Lk is:
(6) |
All the CHs in other layers have to transmit data generated by them as well as data originated from outer layers. Therefore, the energy consumption per unit time of all nodes in Li (1≤i≤k) is:
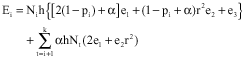 | (7) |
Ideally, when the energy consumption of all the layers is equal, the network lifetime and the energy efficiency are maximized, That is,
E1 = E2 = E3 …. = Ek | (8) |
If let
Ek = Ek-1 | (9) |
Then we can obtain:
(10) |
Let Si stand for the area of layer Li. Then the node density is given by
(11) |
By Eq. 10 and 11, the ratio between the node densities of Li and Li-1 is obtained as:
(12) |
Thus, if distribution densities of nodes between Lk and Lk-1 is deployed by Eq. 12, energy consumption of two layers is balanced. If let
Ek = Ek-2 | (13) |
(14) |
Then,
(15) |
(16) |
After iterative calculating, we can obtain the ratios of ρk, ρk-1, … ρi … ρ2, ρ1. The nodes’ distribution densities of whole network under energy-balancing is achieved when the ρk is determined. Therefore, the more uniform energy dissipation and the longer lifetime of networks are obtained by this energy-balancing layered algorithm.
 | |
| Fig. 3: | Inter-cluster data transmission algorithm |
Data transmission mechanism: The data transmission mechanism of EB-UCP is based on unequal clustering algorithm and energy-balancing layered algorithm. Firstly, sensor nodes can be deployed according to the distribution density based on the results derived in the previous section. Then, nodes use the unequal clustering algorithm to compete CH. When CHs deliver their data to the sink node, each CH first aggregates the data from its cluster members and then sends the packets to the sink node via a multihop path through other intermediate CHs. Thus the data transmission of whole network includes inter-cluster and intra-cluster data transmission. The organization of intra-cluster data transmission is similar to LEACH after clusters have been set up, so it was omitted in this section. The pseudocode of the inter-cluster algorithm for CHi is presented in Fig. 3. In order to gain balanced energy depletion among the CHs, the CH i selects one relay CH with maximum energy resource. When selecting the relay CH with maximum residual energy, the CHi has to exchange energy information with all candidate relay CHs in lines 7-10 of Fig. 3. If there is more than one candidate with the same maximum residual energy, choose one of them randomly. After the CH i selects the relay CH, it forwards data of its own as well as those from the upper layer CHs in lines 11-19. And the selected relay CH will repeat this process until the data arrive at sink node.
Analysis of EB-UCP complexity: The EB-UCP is composed of CH competitive algorithm, energy-balancing layered algorithm and inter-cluster data transmission mechanism. Since energy-balancing layered algorithm can be calculated by sink n ode, we only consider the clustering algorithm and inter-cluster data transmission algorithm. According to previous sections, both algorithm are message-driven, thus we discuss its message complexity. For CH competitive algorithm, Nixpi tentative CHs are produced in every layer and each of them broadcasts a CompeteCH_msg. Then each of them makes a decision by broadcasting a FinalCH_msg to act as a final CH, or a QuitEle_msg to act as an ordinary node. Suppose s CHs are selected, they send out s CH_ADV_msg and then (Ni-s) ordinary nodes transmit (Ni-s) JOIN_CLUSTER_msg. Thus the messages add up to 2Nixpi+s+Ni-s = (2pi+1)Ni, i.e., O (Ni). The inter-cluster data transmission mechanism mainly includes energy inquiring message and data forwarding message. The message complexity of both is O (Ni2). Therefore, the complexity of EB-UCP is O(N12).
SIMULATION RESULTS
Here, the performance of the EB-UCP protocol with simulations is evaluated. Lifetime is the criterion for evaluating the performance of WSNs. In the simulation, we measure the lifetime in terms of the round when the first node dies (Chang and Tassiulas, 2004). For simplicity, an ideal MAC layer and error-free communication links are assumed. The simulation parameters for our proposed protocol are given in Table 1. The experiments described in this part have been conducted with the aid of a well known simulation tool, Ns2. The parameters and characteristics of our architecture are first observed and then the performance of proposed idea is examined comparing with the EEUC and LEACH.
The value of k verification: The suitable number of layers is important to the energy consumption. Too big or too small value of k will decrease the lifetime of network. From Fig. 4, the value of k is 7 which is suitable for the range of 6-8.
Impact of node number of the first layer: In order to investigate the impact of node number of the first layer, its range is varied from 8 to 52 and the aggregation coefficient (α = 0.1, 05, 1) is adopted as shown in Fig. 5. Figure 5 shows that the rounds of lifetime increase almost proportionally for EB-UCP as the number of nodes in the first layer increases. With more CHs closer to the sink node, the lifetime of the network improves significantly. In addition, when CH forward 10% of the cluster load (α = 0.1), the maximum rounds of lifetime is increased by 1-2 times than α = 0.5.
| Table 1: | Parameters of simulations |
 | |
 | |
| Fig. 4: | The value of k verification |
 | |
| Fig. 5: | Impact of node number of the first layer |
Energy efficiency: In this subsection, the performance of EB-UCP, EEUC and LEACH in terms of network lifetime are compared. From Fig. 6a-d, the ratio of alive nodes of EB-UCP is much bigger than LEACH and EEUC when CHs forward different ratio of the cluster load (α = 0.1, 0.2, 0.7, 1.0). Compared with the EB-UCP and EEUC, CHs in LEACH sends their packets to the sink node via single hop and the energy consumption is much higher. In EB-UCP and EEUC, CHs transmit their data to the sink node via multihop, thus a considerable amount of energy is saved. By node distribution of energy balancing in each layer, the energy dissipation of EB-UCP is more uniform than EEUC and LEACH. On average, EB-UCP achieves a 33-54% improvement in network lifetime against EEUC and LEACH depending on the aggregation efficiency.
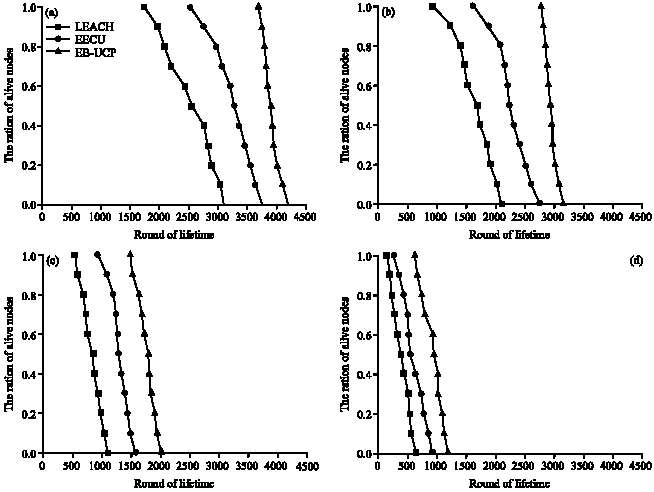 | |
| Fig. 6: | Performance comparison, (a) α = 0.1, (b) α = 0.3, (c) α = 0.7 and (d) α = 1 |
CONCLUSION
The hot spot problem appears when employing the multihop routing in a clustering approach. To address the problem, a novel energy-balancing unequal clustering protocol for WSNs has been introduced. An unequal clustering algorithm from probability view is presented and clusters closer to the sink node have smaller sizes than those farther away from the sink node. Thus CHs closer to the sink node can preserve some energy for the purpose of inter-cluster data forwarding. Then, the balance of energy consumption among layers is analyzed and an energy-balancing layered algorithm is proposed. Based on the above, the data transmission mechanism is discussed. By unequal clustering and node distribution of energy balancing, EB-UCP ensures more balanced energy consumption as well as network lifetime than previous researches. Simulation results show that EB-UCP significantly improves the network lifetime over LEACH and EEUC.
To ease the analysis of EB-UCP, several simplifying assumptions that have been made in this study will be addressed in further research. For example, the effect of errors and collisions and event-based networks where the data generation rate at each node is a function of phenomena in the environment rather than constant at each node will be considered in EB-UCP.
ACKNOWLEDGMENTS
This research was financially supported by National Natural Science Fund of China with grant No. 60472074 and China’s Next Generation Internet Demonstration Project with grant No.CNGI-04-2-1D.
REFERENCES
- Chang, J. and L. Tassiulas, 2004. Maximum lifetime routing in wireless sensor networks. IEEE/ACM Trans. Network., 12: 609-619.
CrossRefDirect Link - De, S., A. Caruso, T. Chaira and S. Chessa, 2006. Bounds on hop distance in greedy routing approach in wireless ad hoc networks. Inter. J. Wirel. Mobile Comput., 1: 131-140.
CrossRefDirect Link - Heinzelman, W.B., A.P. Chandrakasan and H. Balakrishnan, 2002. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wireless Commun., 1: 660-670.
CrossRefDirect Link - Li, C., M. Ye, G. Chen and J. Wu, 2005. An energy-efficient unequal clustering mechanism for wireless sensor networks. Proceedings of the International Conference on Mobile Adhoc and Sensor Systems Conference, November 7-10, 2005, Washington, DC., USA., pp: 1-8.
CrossRefDirect Link - Li, J. and P. Mohapatra, 2005. An analytical model for the energy hole problem in many-to-one sensor networks. Proceedings of the 62nd Semiannual Vehicular Technology Conference, September 25-28, 2005, IEEE Press, Dallas, USA., pp: 2721-2725.
CrossRefDirect Link - Olariu, S. and I. Stojmenovic, 2006. Design guidelines for maximizing lifetime and avoiding energy holes in sensor networks with uniform distribution and uniform reporting. Proceedings of the 25th International Conference on Computer Communications, April 23-29, 2006, Barcelona, Spain, pp: 1-12.
CrossRefDirect Link - Perillo, M., Z. Cheng and W. Heinzelman, 2005. An analysis of strategies for mitigating the sensor network hot spot problem. Proceedings of the 2nd Annual International Conference on Mobile and Ubiquitous Systems: Networking and Services, July 17-21, 2005, IEEE Computer Society, San Diego, USA., pp: 474-478.
CrossRefDirect Link - Perillo, M., C. Zhao and W. Heinzelman, 2004. On the problem of unbalanced load distribution in wireless sensor networks. Proceedings of the Global Telecommunications Conference Workshops 2004, November 29-December 3, 2004, IEEE Press, Dallas, USA., pp: 74-79.
CrossRefDirect Link - Soro, S. and W.B. Heinzelman, 2005. Prolonging the lifetime of wireless sensor networks via unequal clustering. Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium, April 4-8, 2005, Denver, CO., USA., pp: 236-240.
CrossRef








