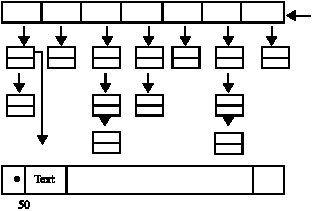
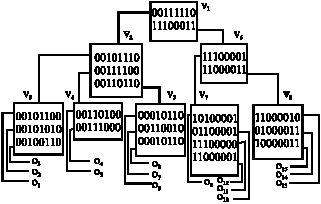
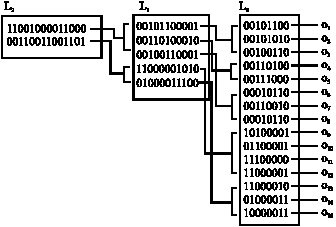
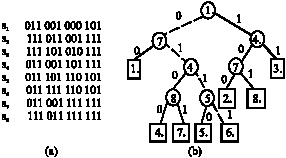
Research Article
An Index Structure for Fast Query Retrieval in Object Oriented Data Bases Using Signature Weight Declustering
Department of Computer Science, Avinashilingam University for Women, Coimbatore, India
R. Nadarajan
Department of Mathematics and Computer Applications, PSG College of Technology, Coimbatore, India