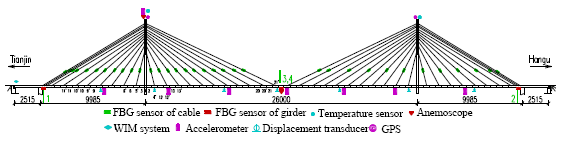
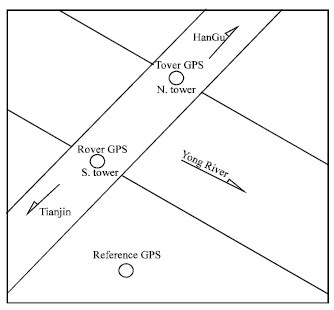
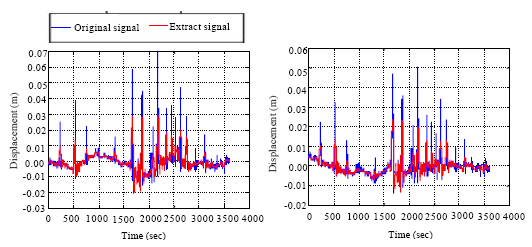
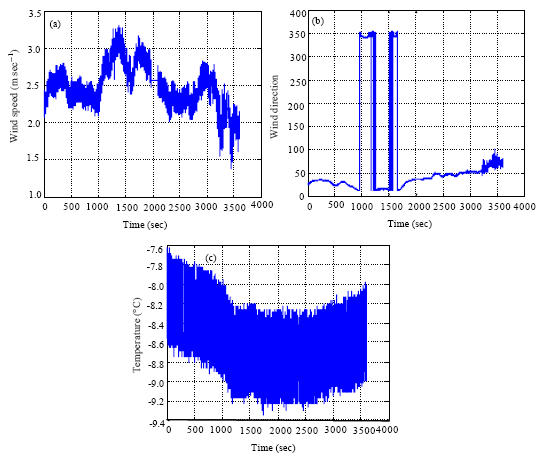
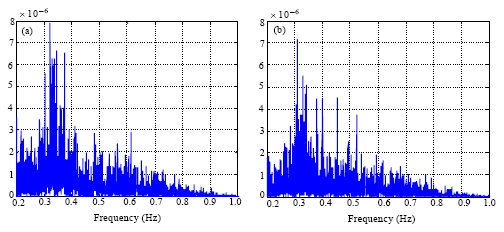
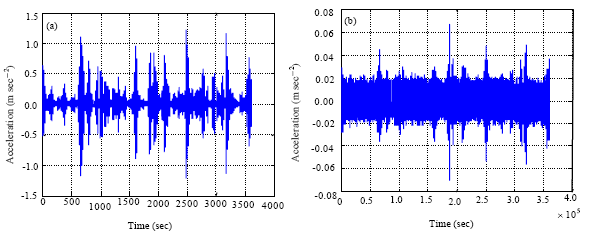
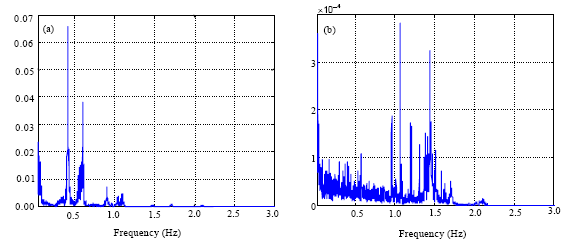
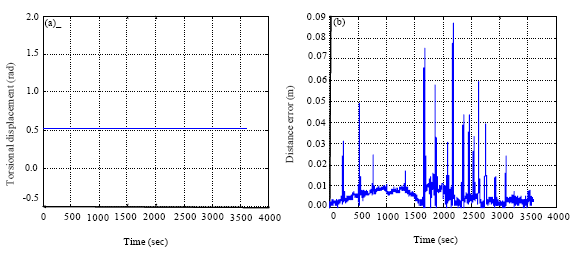
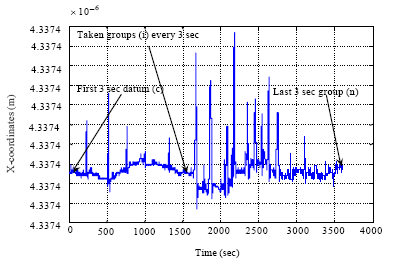
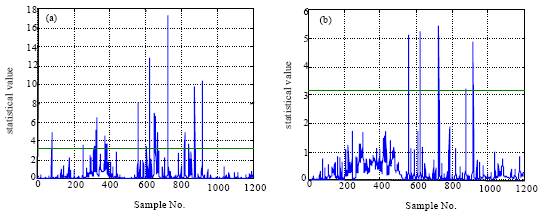
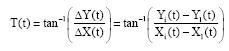Research Article
Tower Bridge Movement Analysis with GPS and Accelerometer Techniques: Case Study Yonghe Tower Bridge
School of Civil Engineering, Harbin Institute of Technology, Harbin, 150090, China
Hui Li
School of Civil Engineering, Harbin Institute of Technology, Harbin, 150090, China