Research Article
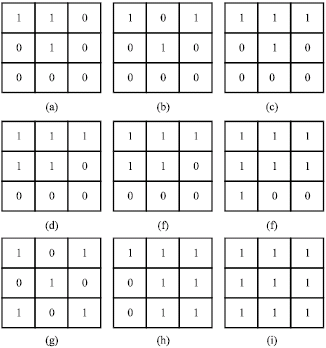
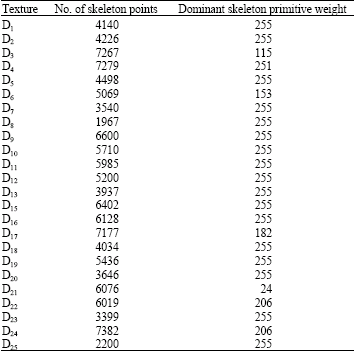
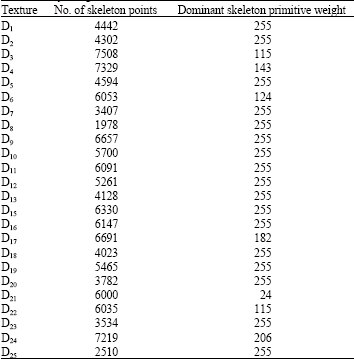
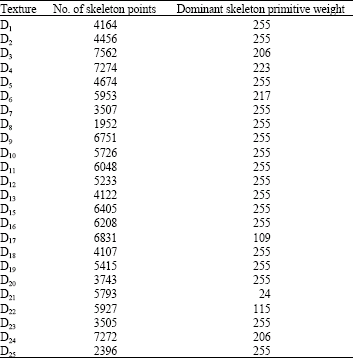
Texture Classification Based on Extraction of Skeleton Primitives Using Wavelets
Department of CSE and IT, Godavari Institute of Engineering and Technology, Rajahmundry, Andra Pradash, India
B. Eswara Reddy
Department of CSE, JNTU College of Engineering, Anantapur, Andra Pradash, India
V. Vijaya Kumar
Department of CSE and IT, Godavari Institute of Engineering and Technology, Rajahmundry, Andra Pradash, India
B. Sujatha
Department of CSE and IT, Godavari Institute of Engineering and Technology, Rajahmundry, Andra Pradash, India