Research Article
Finding Linear Equivalence of Keystream Generators Using Genetic Simulated Annealing
Department of Information Systems, College of Information Technology, University of Bahrain, P.O. Box 32038, Sakhair, Bahrain
Stream ciphers play important role in cryptographic practices and generated pseudorandom sequences with good properties are essential components in a wide variety of modern applications such as radar. Stream cipher is a different class from block cipher that can operate one data unit as small as a bit or a character (Schneier, 1996). Every stream cryptosystem consist of two parts, which are:
| • | Key stream generator and |
| • | Mixer (XOR for the binary sequence). |
A key stream generator outputs a stream of bits (key stream), which is xored with a stream of plaintext bits to produce the stream of cipher text. Mainly, stream cipher systems can be classified into linear and nonlinear stream ciphers. In the linear ciphers, the key stream generators are linear feedback shift registers (LFSRs) which are shift register with linear feedback functions called characteristics polynomials, while, in nonlinear ciphers, the key stream generators are composed of a number of LFSRs combined using a nonlinear combination function, or composed of a shift register with a nonlinear feedback function, which is called nonlinear filter.
The stream cipher system`s security depends entirely on the inside of key stram generator. The security of this generator can be analyzed in terms of randomness, linear complexity and correlation immunity. Thus, good stream cryptosystems must have the following features (Zeng et al., 1991).
| • | They generate long period key streams from short keys. |
| • | Their key streams are random and of large linear complexity. |
| • | They have high degrees of correlation immunity. |
Linear complexity is a well-known complexity measure in the theory of stream ciphers, which is first studied by Massey (1969). Linear complexity of a key stream s is the length of the shortest LFSR which will produce the stream s, which is denoted by L(s). If the value of L(s) is L, then 2L consecutive bits can be used to reconstruct the whole sequence. Hence, to avoid the key stream reconstruction, the value of L should be large.
Linear complexity plays a crucial role in designing good stream cipher systems. Therefore, it has been studied by various authors; some researchers concentrate on finding upper or lower bounds on the linear complexity such as (Caballero-Gil, 2000). Garcia and Fuster-Sabater (2000) concentrate on analyzing the linear complexity of nonlinear filter key stream generators, who mentioned in their paper that there is no efficient method to determine the value of linear complexity of the sequence generated by nonlinear filtering applied to LFSR.
This study is to present a new approach for solving the problem of finding the linear equivalence. Our goal is to find an effective method that can be used to find the linear equivalence and hence the value of linear complexity, for any binary sequence. Therefore, three algorithms have been developed which are based on Simulated Annealing (SA) and Genetic Algorithm (GA). This study includes the description of the proposed algorithms, study of the effectiveness and performance of these algorithms, in addition to a comparison between SA and GA.
SIMULATED ANNEALING AND GENETIC ALGORITHMS
Kirkpatrik et al. (1983) introduced SA as a global optimization heuristic that is inspired by the annealing process in metallurgy. At high temperatures, the molecules of liquid move freely with respect to one another. If the liquid is cooled slowly, thermal mobility is lost. SA is a general randomization technique for solving optimization problems. This technique can help to avoid the problem of getting stuck in a local minimum and to lead towards the globally optimum solution (Yong et al., 1995). In SA, the solution starts with a high temperature and a sequence of trail vectors are generated until inner thermal equilibrium is reached. Once the thermal equilibrium is reached at a particular temperature, the temperature is reduced and a new sequence of moves will start. This process is continued until a sufficiently low temperature is reached, at which no further improvement in the objective function can be achieved (Cheng et al., 2007). Thus, SA algorithm consists of: configurations, re-configuration technique, cost function and cooling schedule.
Many researchers explored the application of SA on many different types of problems, such as cryptographic problems. It has been used, for example, to design S-boxes and Boolean functions (Clark et al., 2004, 2005; Clark and Jacob, 2004) and attacking cipher systems (Golic et al., 1996).
SA can be integrated with GA in order to work on a population of individuals and to preserve good individuals into the next generation (Yong et al., 1995; Sadegheih, 2007; Wong et al., 2005). GA (Holland, 1975; Goldberg, 1989) is a general, probabilistic and adaptive search algorithm. GA is a stochastic search algorithm that is based on the Darwinian principle of survival of the fittest. It works on population of individuals (chromosomes) that represent the candidate solutions. GA can be summarized as follows:
| • | Determine a representation scheme for the candidate solutions. |
| • | Generate the initial population randomly. |
| • | Evaluate the fitness for each chromosome. |
| • | Select members of the population for crossover and mutation to produce a population of children. |
| • | Repeat steps (3-4) until stopping criteria is satisfied. |
GENETIC METHOD
First, we are going to describe GA used to solve the problem under study. The following is the description of GA for finding the linear equivalence.
Representation scheme: In the GA method, variable length chromosomes are used. The binary representation has been chosen to represent the chromosomes that represent the characteristic polynomials of LFSRs. These chromosomes are the candidate linear equivalences for a given key stream of length (lenkey) which is supposed to be 2 L. The minimum chromosome length is 2 bits and the maximum length is lenkey bits.
Fitness function: Fitness function is used to evaluate each chromosome c. In the proposed method, the fitness function is given by Eq. 1.
| Fit(c) = (lenkey-er) + (lenkey/3)*(1.0/(1.0 + l(c))) | (1) |
The fitness value of each chromosome c is assigned by applying the following algorithm:
Algorithm fitness value calculation:
Input: The first lenkey bits of the Keystream and c.
Output: Fitness value of c.
 |
The fitness function includes two terms, the first term (lenkey-er) is to evaluate the correctness of the generated key stream and hence the LFSR. The second term is to evaluate the optimal solution, which is the shortest LFSR. This measure is weighted by (lenkey/3) which has been chosen since it gives the best result.
GA parameter: The genetic operation used to update the population is 1-point crossover and mutation with probability 5%. The selection strategy, used to select chromosomes for the genetic operations, is the 2-tournament selection. The population size (n) is dependent on the length of known key stream (lenkey). The population size n increases as lenkey is increased. Therefore, the population size is computed using Eq. 2.
n = lenkey * 10 | (2) |
The old population is completely replaced by the new population which is generated from the old population by applying the genetic operations. The worst chromosome in the new population is replaced by the best chromosome of the old population.
Stopping criteria: The run of GA is stopped after a fixed number of generations. The solution is the best chromosome in the last generation. The solution should be of fitness value (Lenkey + L), which indicates that the generated key stream is free of error and the chromosome represents the shortest LFSR, i.e., linear equivalence.
GENETIC SIMULATED ANNEALING METHODS
This part of research is to describe the proposed genetic annealing algorithms (GSA1) and (GSA2) for finding the linear equivalence. The representation scheme of the chromosomes, genetic parameters and the fitness functions of genetic method are also used in GSA1 and GSA2. The following are the algorithms. You can see the difference between the two algorithms; the first one is population-oriented and the second one is chromosome-oriented.
Algorithm GSA1:
Generate the initial population (pop) and evaluate it.
 |
Algorithm GSA2:
Generate the initial population (pop) and evaluate it.
 |
EXPERIMENTAL RESULTS
The main purpose of this paper is to study the effectiveness of GSA to solve the problem of finding the linear equivalence of key stream generators. Therefore, the proposed methods have been implemented using C++ programming language and eleven different key streams of different linear complexities, from 3 to 13, have been used as input. These key streams have been generated by LFSRs of characteristics polynomials shown in Table 1. The maximum number of generations used is 30 generations and the input key stream length is 2L bits.
| Table 1: | LFSRs used in the experiments |
 | |
| Table 2: | The probability of algorithms` success (P) |
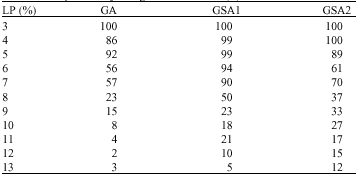 | |
Table 2 shows the probability of success (P). P is calculated by executing the proposed methods 100 times for each key stream (100 trails) and the method success to find the solution if the best chromosome of the last generation is the desired LFSR, i.e., shortest LFSR that generates the given key stream.
First of all, we can see that P decreases as L increases using all methods. This result was expected, that is because, as L increases longer key stream (of length 2L) is required to be tested by the fitness function. But this result may be improved by increasing the number of maximum generations or population size. Furthermore, the integration of SA and GA has improved the performance, such that, the probability of success of GSA1 and GSA2 is greater than of GA and GSA2 gives better results for large linear complexities comparable with GSA1.
New methods for finding the linear equivalence (and the value of linear complexity) for any Binary key stream knowing the first 2L bits have been developed. These methods are based on interesting intelligent techniques which are GA and SA. The results show that GA and SA are capable of solving the underlying problem, but an integration of SA and GA gives better results, that is, the probability of success is increased by using SA.