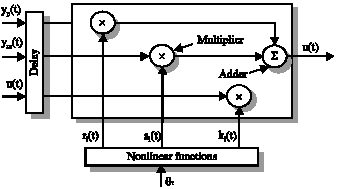
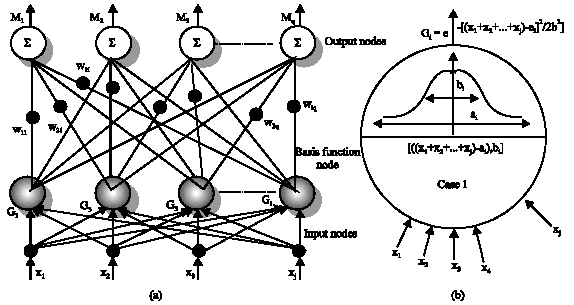
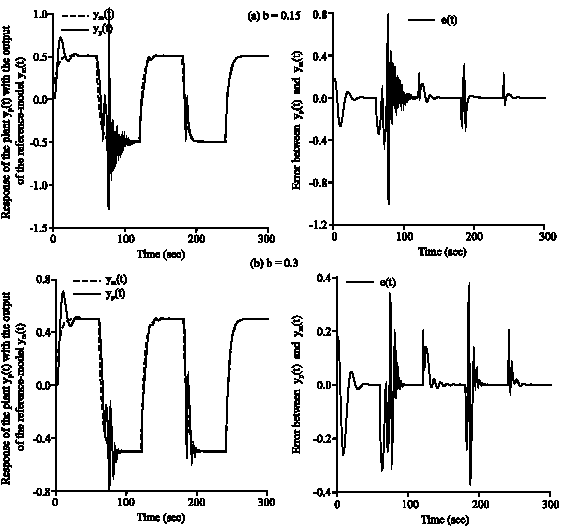
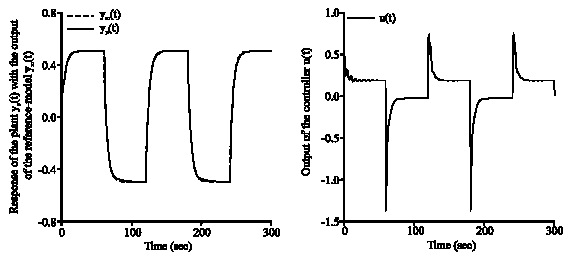
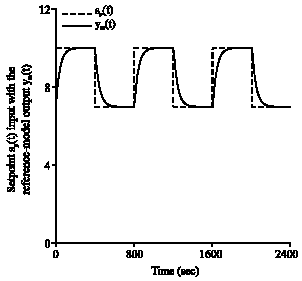
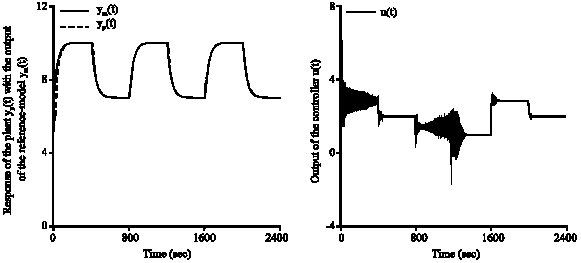
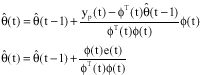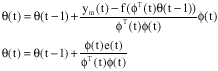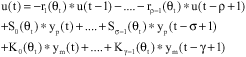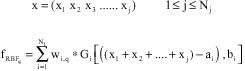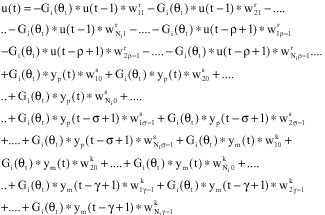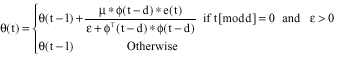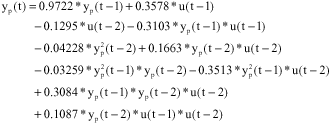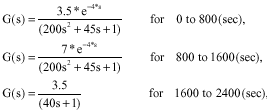Research Article
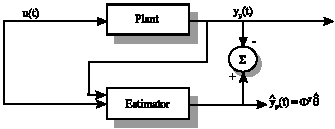
A Radial Basic Function with Multiple Input and Multiple Output Neural Network to Control a Non-Linear Plant of Unknown Dynamics
Department of Electronic and Communication Engineering, Faculty of Mechanical and Electrical Engineering, Damascus University, Syria
G.A. Salman
College of Computer Engineering and Information, Syrian National Private University for Science and Technology, Syria