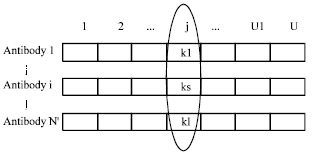
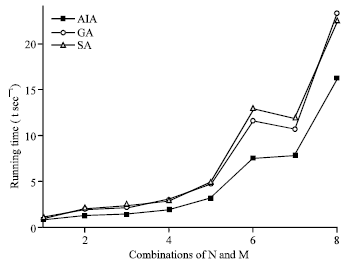
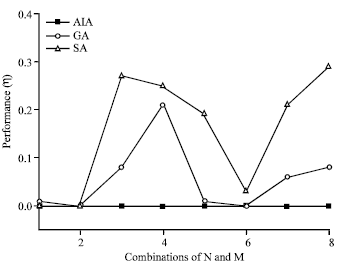
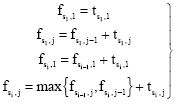Research Article
Improved Artificial Immune Algorithm and its application on the Permutation Flow Shop Sequencing Problems
Software Engineering Institute, Xidian University, Xi`an 710071, China
Xiyang Liu
Software Engineering Institute, Xidian University, Xi`an 710071, China