Research Article
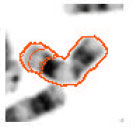
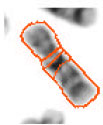
Discrete Cosine Transform Based Gradient Vector Flow Active Contours for Chromosome Image Segmentation-an Analysis
Center for Medical Electronics, Department of Electronics and Communication Engineering, Anna University, Chennai 600025, India
G. Ravindran
Faculty of Information and Communication Engineering, Anna University, Chennai 600025, India