Research Article
K- Means Clustering Based Image Compression in Wavelet Domain
Department of Electronics and Communication Engineering, Sri Venkateswara College of Engineering. Sriperumbudur-602 105, India
Y.V. Ramana Rao
Department of Electronics and Communication Engineering, College of Engineering, Anna University, Chennai-600 025, India









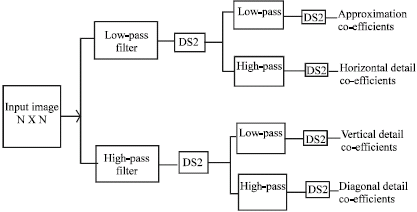
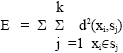
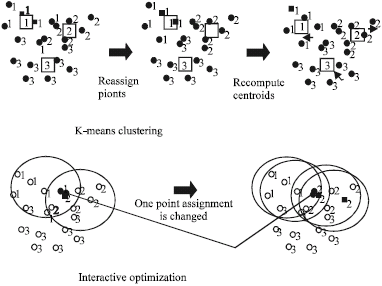

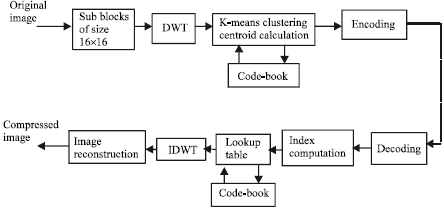

shree Reply
hi sir/mam,
im studying mphil cs in my research i can select image compression . i read ur paper its very usefull for me really nice .its a new innovative for image compression side . can u plz send me the code for refer my research work its very useful for my research plz