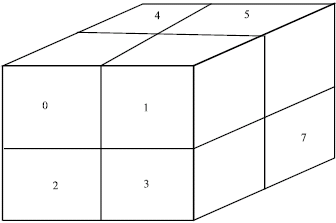
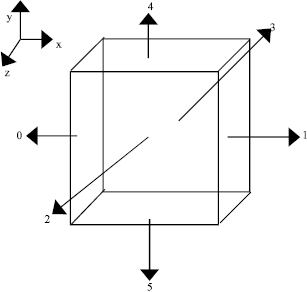
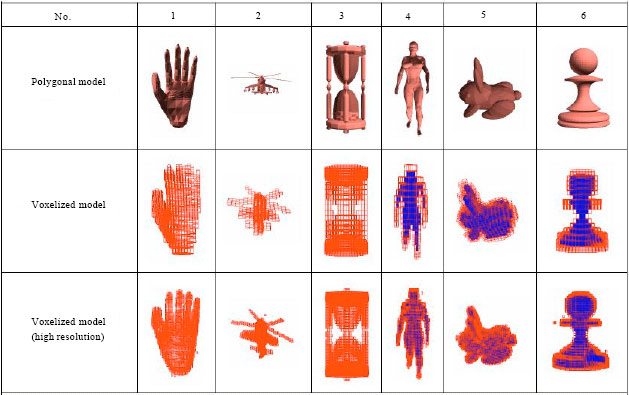
Research Article
A New Method on Voxelizing Triangular Mesh Model
Department of Computer Science and Technology, Xi`an Jiaotong University, Xi`an, China
Zheng Qin
Department of Computer Science and Technology, Xi`an Jiaotong University, Xi`an, China
Junying Chen
Department of Computer Science and Technology, Xi`an Jiaotong University, Xi`an, China