Research Article
Introduction to Multitone Multiresolution Wavelet Analysis
Theta Networks, 25 XiaoYun Road, San Yuan East Bridge, Beijing 100027, China
FROM FOURIER TRANSFORM TO WAVELET TRANSFORM
Background: A signal or function x(t) can often be analyzed, described or processed if expressed as a linear decomposition by Burrus et al. (1998), Cohen and Kovacevic (1996) and Anonymous (1997):
| (1) |
Where, k is an integer index for finite or infinite sum, {ak} are the expansion coefficients, may be referred to as transform domain ![]() {.}, {φk(t)} are the expansion set. If the expansion in Eq. (1) is unique, the set is called a basis. If the basis is orthogonal, then the normal coefficients can be calculated by the inner product (Burrus et al., 1998; Cohen and Kovacevic, 1996; Anonymous, 1997):
{.}, {φk(t)} are the expansion set. If the expansion in Eq. (1) is unique, the set is called a basis. If the basis is orthogonal, then the normal coefficients can be calculated by the inner product (Burrus et al., 1998; Cohen and Kovacevic, 1996; Anonymous, 1997):
| (2) |
The function x(t) was traditionally represented by defining its value for each value of t in the domain of the function. Then x(t) may represented as a linear combination (a weighted sum) of delta functions δ(t). Thus, the basis functions {φk(t)} in Eq. (1) became the well-known (Kronecker) delta function δ(t) (Damper, 1995).
THE FOURIER TRANSFORM
The fourier transform allows us to find a new representation for the function, given by the coefficients of complex exponentials of integer multiples of some fundamental frequency (Damper, 1995; Korner, 1988 ). In other words, the fourier transform is simply a change of basis from the basis of delta functions δ(t) to the basis of complex sinusoids ejwt. The continuous-time transformed to the frequency domain by Korner (1988), Haykin and Van Veen (1999):
| (3) |
This fourier transform is mainly used for theoretical analysis and design of continuous signals and systems. However, advances in computer and digital technology resulted the Discrete fourier Transform (DFT) defined by Eq. 2.20 and 2.21 (Damper, 1995; Haykin and Van Veen, 1999). It may be noted that DFT bases exhibit the desired orthogonality that make it attractive for multitone transmission. By using Eq. 2.10, it is easy to prove that (Hakin and Van Veen, 1999):
| (4) |
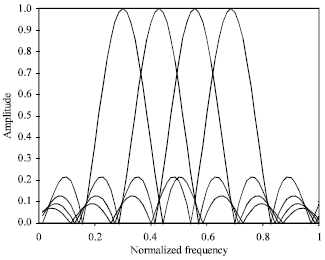
Where, k1 and k2 are integers. Frequency domain basis are shown in Fig. 1 (four only). DFT bases have rectangular time-shape that result in a sinc frequency characteristics.
Therefore, the DFT bases used by Discrete Multitone Modulation (DMT) has the serious shortcoming of poor stop-band attenuation (–13 dB only). DMT is the standard modulation scheme chose for ADSL modems and approved by ITU in July 1999, known as G992.1.
 | |
| Fig. 1: | Frequency-domain bases (four only) |
Thus, the resultant out-of-band multitone spectrum is relatively slowly decaying as shown in Fig. 1. In Fig. 1, the x-axis is the normalized frequency relative to the element rate of the signal.
THE WINDOWED FOURIER TRANSFORM
The fourier transform gives no information about the locality of the frequency components in time. Thus, in an attempt to add some locality of time to the fourier transform, the sines and cosines are modulated by a window function. This transform is referred to as Short-time Fourier Transform (STFT) (Haykin and Van Veen, 1999; Van Nee and Prasad, 2000; Zhao, 1999; Vitterli and Kovacevic, 1995; Portnoff, 1980; Reza, 1999; Reza, 1999). Then Eq. 3 becomes:
| (5) |
Where, g(t) is the window function and g*(.) denotes the complex conjugate of g(.). Fig. 2 STFT bases using Hanning window (four only). In this case, the bases are shown in Fig. 2 for four bases employing Hanning window. For comparison purposes, the bandwidth occupied by the Hanning bases is assumed to be equal to that for the rectangular. The windowed DMT was discussed in chapter two and the term FMT was used. As shown in Fig. 2 compared to Fig. 1, a lower stop-band attenuation (–31 dB) is gained. The resultant out-of-band spectrum decays faster than that of the DMT which uses DFT basis (Van Nee and Prasad, 2000; Cioffi, 2000).
In addition, the resolution in time and frequency can not be arbitrary small, because their product is lower bounded by the so-called Heisenberg inequality (Haykin and Van Veen, 1999; Reza, 1999; Cioffi, 2000; Morgan, 1997; Hess-Nielsen and Wickerhauser, 1996).
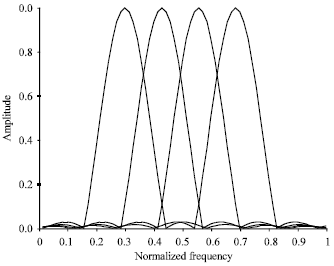 | |
| Fig. 2: | STFT bases using hanning window (four only) |
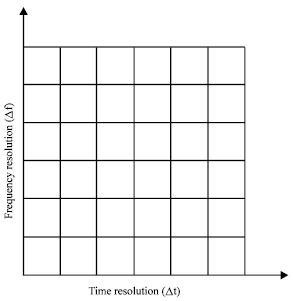 | |
| Fig. 3: | Time-frequency resolution of STFT |
Thus, although the window size can be varied, it is the same for all frequencies once it is chosen. Accordingly, the time and frequency resolutions become fixed for all time instants and frequency bands as shown in Fig. 3 (Haykin and Van Veen, 1999; Reza, 1999; Hess-Nielsen and Wickerhauser, 1996).
THE WAVELET TRANSFORM
To overcome the time-frequency resolution limitation of the STFT, one method is known as the Wavelet Transform (WT) (Burrus et al., 1998; Reza, 1999; Daubechies, 1990). The WT was introduced by the idea that we could vary the scale of the basis functions instead of their frequency. In other words, the fundamental idea behind wavelets is to analyze according to scale (Perkins and Fricke, 2000).
Given a nonstationary function x(t), the WT is defined as the inner product of x(t) with two-parameter set of basis functions given by (Burrus et al., 1998; Cohen and Kovacevic, 1996; Daubechies, 1992):
| (6) |
Where, γ is a scale parameter and τ is a time delay. Thus the WT of x(t) is defined by Burrus et al. (1998) Cohen and Kovacevie (1996) and Daubechies (1992):
| (7) |
In wavelet analysis, the basis function ψτ,γ(t) is an oscillating function; therefore, there is no need to use sines or cosines (waves) as in fourier analysis. While the basis function ejwt in fourier analysis oscillates forever, the basis function ψτ,γ(t) in wavelet analysis is localized in time, it lasts for only a few cycles. The functions ψτ,γ(t) are called wavelets; they constitute the building blocks of the WT. According to Eq. 6, the wavelets are scaled and translated versions of a prototype ψ(t), called the mother wavelet. In terms of filters, the mother wavelet is a bandpass filter in general (Haykin and Van Veen, 1999). For wavelets, the delay parameter τ gives the position of the wavelet ψτ,γ(t), while the scale factor γ governs its frequency content (Daubechies, 1990).
Thus, the wavelet expansion represents a function as a sum of time-shifted τ (translated) and scaled γ (dilated) representations of ψτ,γ(t) instead of representing the function as a sum of weighted delta functions (as in the time domain), or as a sum of weighted sinusoids (as in the frequency domain) (Perkins and Fricke, 2000).
This leads to variable time-scale localization. This variation can be carried out without violation the Heisenberg inequality, by using short windows at high frequencies and long at low frequencies. In filter bank terminology, this is similar to the so-called constant-Q analysis. The time-frequency plane for constant Q filter bank is shown in Fig. 4 ( Hess-Nielsen and Wickerhauser, 1996).
Multiresolution analysis: In order to agree with the previous discussion of scale or resolution, we formulate the basic requirement of Multi-resolution Analysis (MRA). All useful wavelet systems satisfy the multiresolution condition.
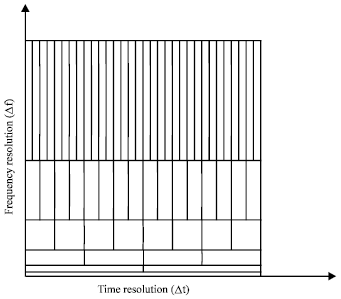 | |
| Fig. 4: | Time-frequency resolution for constant-Q filter bank |
This means that if a set of signals can be represented by a weighted sum of φ(t–k), then a larger set (including the original) can be represented by a weighted sum of φ(2t–k) (Burrus et al., 1998). In order to use the idea of multiresolution, we will start by defining the scaling function (Burrus et al., Cohen and Kovacevic, 1996; Anonymous, 1997; Portnoff, 1980; Morgan, 1997; Daubechies, 1992 ).
The scaling equation is a recursive expression that is used to generate wavelets. A set of scaling functions in terms of integer translates of the basic scaling function are defined by,
| (8) |
Where, L2(R) is the space of all functions x(t) with a well-defined integral of the square of the modulus of the function. The subspace of L2(R) spanned by these functions is defined as,
| (9) |
for all integers k from minus infinity to infinity. The over-bar denotes closure.
One can generally increase the size of the space spanned by changing the time scale of the scaling functions. A 2-dimensional family is generated from the basic scaling function by scaling and translation by:
| (10) |
Whose span over k is:
| (11) |
This means that if x(t) ευj, then it can be expressed as:
| (12) |
In similar way, one can find from Eq. 8-12, the mother wavelet ψ(t) results in the following 2-dimensional discrete-parameterization of ψτ,γ(t), denoted by ψk,j(t):
| (13) |
and x(t) can be expressed as:
| (14) |
MRA formulated by requiring a nesting of the spanned spaces as:
| (15) |
More compactly, Eq. 15 may be written as:
| (16) |
with,
| (17) |
The space that contains high resolution signals will also contain those of lower resolution. Because of the definition of υj, the spaces have to satisfy a natural scaling condition:
| (18) |
which ensures elements in a space are simply scaled versions of the elements in the next space.
The nesting of the spans of φ(2jt–k), denoted by υj and is shown in Eq. 15 and 18, is achieved by requiring that φ(t)ευ1, which means that if φ(t) is in υ0, it is also in υ1, the space spanned by φ(2t). This means φ(t) can be expressed in terms of a weighted sum of shifted φ(2t) as:
| (19) |
with h0(i) being the scaling coefficients and φ(t) being the scaling function which satisfies this equation which is sometimes called the refinement equation, the dilation equation, or the MRA equation.
Similarly, for the wavelet function:
| (20) |
with h1(i) being the wavelet coefficients and ψ(t) being the wavelet function.
THE DISCRETE WAVELET TRANSFORM (DWT)
In many applications, one never has to deal directly with the scaling functions or wavelets. Only the coefficients h0 (i) and h1 (i) in the defining Eq. 19 and 20 need be considered and they can be viewed as digital filters (Burrus et al., 1998; Reza, 1999).
In order to study directly with the wavelet transform coefficients, the relationship between the scaling expansion coefficients at a lower scale level in terms of those at a higher scale will be derived (Burrus et al., 1998), starting with the basic MRA (Eq. 19). Assuming a unique solution exists, scale and translate the time variable gives:
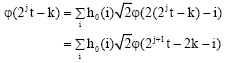 | (21) |
which, after changing variables m = 2k + i, becomes:
| (22) |
Whose, span is Vj,
| (23) |
then,
| (24) |
is expressible at a scale of j+1 with scaling functions only and no wavelets. At one scale lower resolution, wavelets are necessary for the detail not available at a scale of j such that:
| (25) |
Where, 2j/2 term maintain the unity norm of the basis functions at various scales. The coefficients aj(k) and dj(k) in Eq. 25 are called the discrete wavelet transform of the signal x(t). If the wavelet system is orthogonal, then these coefficients are found using Eq. 2. For example the scaling coefficients at level j are:
| (26) |
By using Eq. 22 and interchanging the sum and integral, can be written as:
| (27) |
But the integral is the inner product with the scaling function at a scale of j +1 giving:
| (28) |
The corresponding relationship for the wavelet expansion coefficients is:
| (29) |
Equations 28 and 29 state that the scaling and wavelet coefficients at higher scale, along with the scaling and wavelet filters, h0 (k) and h1 (k), respectively can be used to calculate the wavelet and scaling coefficients, or discrete wavelet transform coefficients at lower scales. Because the filter impulse responses form an orthonormal set, it is very simple to reconstruct the higher resolution expansion coefficients as:
| (30) |
IMPLEMENTATION OF THE WAVELET SYSTEM
The word system is used in communications to describe a set of elements (or functional blocks) that are connected together in such a manner as to achieve a desired objective (Hykin, 2001). The objective of the wavelet system is to implement the wavelet transform as realizable building blocks.
The analysis filter bank efficiently calculates the DWT using banks of digital filters and down-samplers. Similarly, the synthesis filter bank efficiently calculates the inverse DWT by reconstructing the original discrete signal by using up-samplers and banks of digital filters. This is exactly what Eq. 28, 29 and 30 represent (Burrus et al., 1998).
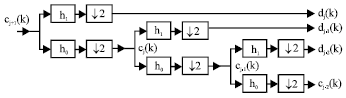 | |
| Fig. 5: | Three-stage wavelet analysis tree |
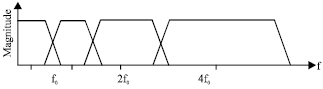 | |
| Fig. 6: | Octave-band frequency response of the analysis filters in Fig. 5 |
The two Eq. 28 and 29 show that the scaling and wavelet coefficients at different levels of scale can be obtained by convolving the expansion coefficients at scale j by the time-reversed recursion coefficients h0(L-1-i) and h1(L-1-i) then down sampling to give the expansion coefficients at the next level of j-1 which is the coarser scale.
The implementation of these Equations is illustrated in the first stage of Fig. 5 where, the down-sampling arrows, ↓2, denote a decimation or down sampling by two and the other boxes denote FIR filtering with a low pass filter denoted by h0(i) and a high pass filter denoted by h1(i) (Burrus et al., 1998). This first stage divides the spectrum of cj+1(k) into a low-pass band and a high-pass band, resulting in scaling coefficients and wavelet coefficients at lower scale cj(k) and dj(k) as also shown in Fig. 5.
The splitting, filtering and decimation can be repeated on the low pass filter output twice again to obtain coarser scaling and wavelet expansion coefficients cj-2 and dj-2. In this case, the frequency responses of the analysis filters in the filter bank are regularly spaced in a logarithmic scale. These filters are naturally distributed into octaves, as shown in Fig. 6.
The original discrete cj+1 can be recovered from its two filtered and sub-sampled versions cj and dj. To do so, both are up-sampled by the operation denoted by, 82, then filtered by g0(i) and g1(i) respectively and finally added together, as shown in Fig. 7. The reconstructed signal is not identical to the original one, unless the filters meet some specific constraints. Filters that meet these constraints are said to have Perfect Reconstruction (PR) property.
For high enough scale, the scaling functions act as delta functions such that φ(t)≡δ(t), with the inner product in Eq. 2 to calculate the high scale coefficients, as simply, a sampling of x(t).
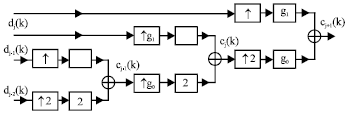 | |
| Fig. 7: | Three-stage wavelet synthesis tree |
This approximation of the scaling coefficients is good if the moments of the scaling function are zero or small and this is usually the case (Burrus et al., 1998).
WAVELET PACKETS
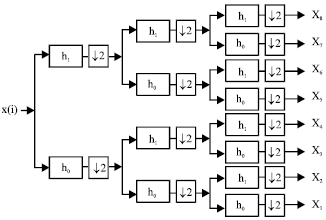
Wavelet packets represent an extension of the classical wavelets which yields basis functions with better frequency localization at the cost of a slightly more expensive transform. In order to generate such a basis system it is necessary to iterate (split and down sample) the highpass wavelet branch of the filter bank algorithm as well as the lowpass scaling function branch. Such splitting operation results in a filter bank structure like a full binary tree that is shown in Fig. 8 (Burrus et al., 1998; Akansu and Smith, 1998). The binary tree structure decomposes the signal x(t) into eight subband signals Xk k = 1,2,…,8. Each of which has energy concentrated in eight equal subbands.
An ![]() -band packet structure implemented using
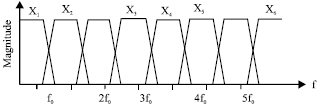
-band packet structure implemented using ![]() levels (Akansu and Smith, 1998). For example, in Fig. 8, the eight-band filter bank is implemented using three levels or three iterations. The corresponding frequency response of the wavelet packet filter bank is shown in Fig. 9.
levels (Akansu and Smith, 1998). For example, in Fig. 8, the eight-band filter bank is implemented using three levels or three iterations. The corresponding frequency response of the wavelet packet filter bank is shown in Fig. 9.
The potential of wavelet packets lies in the capacity to offer a rich menu of basis functions that satisfy PR conditions, from which the best one can be chosen for given application (Vitterli and Kovacevic, 1995).
TRANSMULTIPLEXERS (TMS)
Transmultiplexers were originally presented in the context of converting TDM signals into FDM signals with the goal of converting back to time-domain-multiplexed signals at some later point (Peled and Winograd, 1978; Scheuermann and Gockler, 1981). MCM, as mentioned in chapter one, can be interpreted as a TM (Neurohr and Schilpp, 1998). Therefore, the design of MCM directly related to the design of TM.
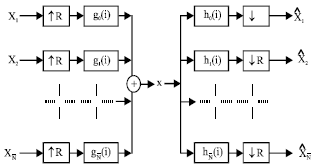
A TM is a multiinput, multioutput, multirate structure. It is essentially exactly opposite to that of the filter bank. It consists of a synthesis filter bank at the input followed by an analysis filter bank at the output end (Mitra, 1998).
 | |
| Fig. 8: | Three-stage wavelet packet filter bank |
 | |
| Fig. 9: | Frequency response of the wavelet packet filter bank of Fig. 8 |
 | |
| Fig. 10: | Transmultiplexer |
A TM is shown in Fig. 10. In the ideal case, that means no distortion and noise added at the channel, the data shall be perfectly recovered in the analysis part of the receiver, such that ![]() = Xk
= Xk
These conditions will be discussed later. There are several possibilities to design PR TMs. The properties of the TM depend on the choice of the set of subcarriers gk(i) and hk(i), the interpolation/decimation factor (R) and bands number (![]() ). In the following discussion four possible TM structures are introduced, which are very important in the design of multicarrier system.
). In the following discussion four possible TM structures are introduced, which are very important in the design of multicarrier system.
BLOCK TRANSFORM (BT)
Thus far, the terms filter bank and transform have been used, but their relationship was not clear. A transform, in general, implies any mapping from one signal into another and so all filter banks are transforms (Akansu and Smith, 1998). But in its common usage in signal processing, it often referred to block transform (BT) given by Akansu and Smith (Akansu and Smith, 1998):
| (31) |
Where, x and X are 1-dimensional column vectors and G is an ![]() x
x![]() matrix of transform basis. DFT is an example of BT, with G defined by Eq. (2.20). In this case, the TM of Fig. 10 is reduced to a transform where H = G* and R =
matrix of transform basis. DFT is an example of BT, with G defined by Eq. (2.20). In this case, the TM of Fig. 10 is reduced to a transform where H = G* and R = ![]() . This is equivalent to inverse/foreword fourier transformation. Thus, it is a DMT transceiver. Fig. 1 shows the frequency response of DMT transmission.
. This is equivalent to inverse/foreword fourier transformation. Thus, it is a DMT transceiver. Fig. 1 shows the frequency response of DMT transmission.
WAVELET PACKET MODULATION (WPM)
Wavelet packet division multiplexing or wavelet packet modulation, (Fig. 11) is essentially, a multiple signal transmission technique in which the input signals are waveform modulated onto wavelet packet basis functions for transmission. The overlapping nature of such waveforms in time and frequency provides a capacity improvement over the commonly used FFT scheme (which is used by DMT modulation), while their orthogonality properties ensure that the overlapping signals can be separated independently in the receiver (Wong, 1997). Therefore, in this thesis WPM is suggested to be used for MTM. The resultant multicarrier system is called DWMT.
The WPM is based on the discrete wavelet packet transform discussed in the previous section. It should be noted that the tree structure of the wavelet packet consists of an elemental two-band TM blocks shown in Fig. 12. This is an important property gained by WPM, which provide significant design simplicity. The overall system design is reduced to the design of a two-band TM and then iterated to form the wavelet packet (Akansu and Smith, 1998).
In addition, tree structures can provide computationally efficient realizations of ![]() -band TMs of Fig. 10. It is interesting to note that they can be implemented in an equivalent
-band TMs of Fig. 10. It is interesting to note that they can be implemented in an equivalent ![]() -band form, often called parallel form implementation (Akansu and Smith, 1998). The key to converting from a tree to parallel form is the use of the multirate principles of migrating filters forward and backward (Crochiere and Rabiner, 1983). For example, the uniform band tree structured TM in Fig. 11, can be implemented in the form of the
-band form, often called parallel form implementation (Akansu and Smith, 1998). The key to converting from a tree to parallel form is the use of the multirate principles of migrating filters forward and backward (Crochiere and Rabiner, 1983). For example, the uniform band tree structured TM in Fig. 11, can be implemented in the form of the ![]() -band parallel form (Akansu and Smith, 1998; Crochiere and Rabiner, 1983):
-band parallel form (Akansu and Smith, 1998; Crochiere and Rabiner, 1983):
| (32) |
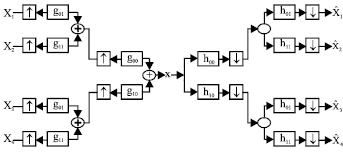 | |
| Fig. 11: | A transmultiplexer implementation of a four-band WPM scheme |
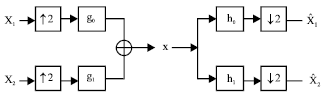 | |
| Fig. 12: | Two-band transmultiplexer |
Where, G(z) denoted the z-transform of g(t). The synthesis filters are found in the same manner. The z-domain representation of the filters do not imply a numeric description of the effective length (Leff)of the overall tree structured TM filter. Therefore, a general formula was derived that calculate the overall effective filter length from its z-domain representation given by ![]() this is:
this is:
| (33) |
Where, j is stage index for a total of S stages. Lj is the length of the jth filter. Note that Eq. 33 includes also the tree structures of non-identical elemental blocks.
For the case of equal filter lengths for all stages, which is the case considered during simulation, the index j from Lj is omitted. Then Eq. 33 is simplified to:
| (34) |
Eq. 34 shows that the effective length of the WPM filters is much larger than the designed prototype two-band filter length. Although this will increase system latency, the advantage is being better frequency characteristics of the subchannels.
LAPPED TRANSFORM
A lapped transform (LT) is a multirate structure, with the synthesis and analysis filters have a particular structure. As in the BT, the system is critically decimated, since R = ![]() .
.
 | |
| Fig. 13: | Hierarchical lapped transform |
For a LT, the synthesis (also the analysis) filters are uniform band FIR filters and they are defined from the columns of the matrix G, in the form (Malvar, 1992):
| (35) |
Where, gk,i is the element in the ith row and kth column of G. The parameter q called the overlap factor, which specifies how many input blocks are used to compute an output block, in the direct transform. When q = 1, the LT reduces to a BT. Therefore the name lapped transform, it is a generalization of a BT, in which the input block is longer than the output block (Malvar, 1992; Queiroz et al., 1996).
Originally LT was proposed by Princen and Bradley (1986). Since then many classes and nomenclatures have been appeared. These include, Lapped Orthogonal Transform (LOT) (Malvar, 1989) (which is the special case with q = 2), Modulated Lapped Transform (MLT) (which is similar to the LOT with cosine-modulated filter bank and thus provide implementation simplicity) and Extended Lapped Transform (ELT) (which is a generalization of MLT with arbitrary long basis functions q >2) (Malvar, 1992).
The LT in its own, is a special case of the generalized WPM. The ![]() -channel lapped transform in Fig. 10 can be described by a
-channel lapped transform in Fig. 10 can be described by a ![]() -branch single-stage tree (Neurohr and Schilpp, 1998). For multistage tree, the value of q may be non-integer value, which is the case for Hierarchical Lapped Transform.
-branch single-stage tree (Neurohr and Schilpp, 1998). For multistage tree, the value of q may be non-integer value, which is the case for Hierarchical Lapped Transform.
HIERARCHICAL LAPPED TRANSFORM (HLT)
HLT is a tree-structured LT. Specifically, the HLT is essentially WPM, but with two-band building blocks being lapped transformed and then cascaded by connecting them hierarchically and hence the name HLT. The HLT in general, divides the frequency band nonuniformly among the filters (and thus the subchannels). Nonuniform DWMT allows a variable partitioning of the channel with respect to the channel frequency response. The time-frequency diagram and the tree diagram describing the hierarchical connection are shown in Fig. 13 (Neurohr and Schilpp, 1998).
S.G.VENKATESH Reply
This paper gives the introduction part in a very good form. It gives a basic platform for the beginners who are eager to do research in the field of wavelet theory. It will be more useful to me if i get the papers of Daubecies work namely " Ten lectures on wavelets" and "compactly supported orthonormal wavelets"
thanking u.