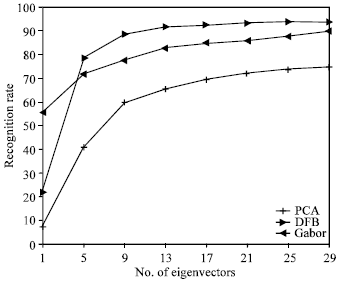
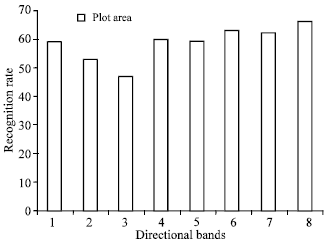
Research Article
Principal Component Analysis of Directional Images for Face Recognition
Department of Electrical Engineering, COMSATS Institute of Information Technology, Sector H-811, Islamabad, Pakistan
Muhammad Khalid Khan
Department of Computer Science, International Islamic University, Islamabad, Pakistan
Muhammad Aurangzeb Khan
Department of Computer Science, International Islamic University, Islamabad, Pakistan
Muhammad Talal Ibrahim
Department of Software Engineering, Army Public College of Management and Engineering Sciences, Rawalpindi, Pakistan
Muhammad Kamran Ahmed
Department of Software Engineering, Army Public College of Management and Engineering Sciences, Rawalpindi, Pakistan
Jahanzeb Afzal Baig
Department of Software Engineering, Army Public College of Management and Engineering Sciences, Rawalpindi, Pakistan