Research Article
Magneto-rotatory Thermal Convection in Couple-stress Fluid
Department of Mathematics, ICDEOL, Himachal Pradesh University, Summer Hill, Shimla-171005, India
A comprehensive account of thermal instability (Bénard convection) in a fluid layer under varying assumptions of hydrodynamics has been summarized in the celebrated monograph by Chandrasekhar (1981). Abdul-Bari and Al-Rubai (2008) have studied the influence of Rayleigh-number in turbulent and laminar region in parallel-plate vertical channels. The influence of radiation on the unsteady free convection flow of a viscous incompressible fluid past a moving vertical plate with Newtonian heating has been investigated theoretically by Narahari and Ishak (2011). Admon et al. (2011) have considered the unsteady free convection flow near the stagnation point of a three-dimensional body. The theory of couple-stress fluid has been formulated by Stokes (1966). One of the applications of couple-stress fluid is its use to the study of the mechanisms of lubrications of synovial joints, which has become the object of scientific research. A human joint is a dynamically loaded bearing which has articular cartilage as the bearing and synovial fluid as the lubricant. When a fluid is generated, squeeze-film action is capable of providing considerable protection to the cartilage surface. The shoulder, ankle, knee and hip joints are the loaded-bearing synovial joints of the human body and these joints have a low friction coefficient and negligible wear. Normal synovial fluid is a viscous, non-Newtonian fluid and is generally clear or yellowish. According to the theory of Stokes, couple-stresses appear in noticeable magnitudes in fluids with very large molecules.
Many of the flow problems in fluids with couple-stresses, discussed by Stokes, indicate some possible experiments, which could be used for determining the material constants and the results are found to differ from those of Newtonian fluid. Couple-stresses are found to appear in noticeable magnitudes in polymer solutions for force and couple-stresses. This theory is developed in an effort to examine the simplest generalization of the classical theory, which would allow polar effects. The constitutive equations proposed by Stokes (1966) are:
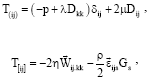 |
and:
Where:
and:
Here, Tij, T(ij), T[ij], Mij, Dij, ![]() , Gs,
, Gs, ![]() , V, ρ and λ, μ, η, η', are stress tensor, symmetric part of Tij anti-symmetric part of Tij the couple-stress tensor, deformation tensor, the vorticity tensor, the vorticity vector, body couple, the alternating unit tensor, velocity field, the density and material constants, respectively. The dimensions of λ and μ are those of viscosity whereas the dimensions of η and η' are those of momentum.
, V, ρ and λ, μ, η, η', are stress tensor, symmetric part of Tij anti-symmetric part of Tij the couple-stress tensor, deformation tensor, the vorticity tensor, the vorticity vector, body couple, the alternating unit tensor, velocity field, the density and material constants, respectively. The dimensions of λ and μ are those of viscosity whereas the dimensions of η and η' are those of momentum.
Since the long chain hyaluronic acid molecules are found as additives in synovial fluids, Walicki and Walicka (1999) modeled the synovial fluid as a couple-stress fluid. The synovial fluid is the natural lubricant of joints of the vertebrates. The detailed description of the joint lubrication has very important practical implications. Practically all diseases of joints are caused by or connected with a malfunction of the lubrication. The efficiency of the physiological joint lubrication is caused by sefveral mechanisms. The synovial fluid is, due to its content of the hyaluronic acid, a fluid of high viscosity, near to a gel. Goel et al. (1999) have studied the hydromagnetic stability of an unbounded couple-stress binary fluid mixture under rotation with vertical temperature and concentration gradients. Sharma et al. (2002) have considered a couple-stress fluid with suspended particles heated from below. They have found that for stationary convection, couple-stress has a stabilizing effect whereas suspended particles have a destabilizing effect. The peristaltic flow of blood through a planar channel of uniform thickness has been investigated by Sobh and Oda (2008). A layer of such fluid heated from below under the action of magnetic field and rotation may find applications in physiological processes e.g., MHD finds applications in physiological processes such as magnetic therapy; heating, rotation may find applications in physio-therapy.
Keeping in mind the importance of couple-stress fluid, convection in fluid layer heated from below, magnetic field and rotation; the present paper attempts to study the effect of uniform vertical magnetic field on the couple-stress fluid heated from below in the presence of a uniform rotation.
FORMULATION OF THE PROBLEM AND PERTURBATION EQUATIONS
Consider an infinite, horizontal, incompressible, electrically conducting couple-stress fluid layer of thickness, heated from below so that, the temperatures and densities at the bottom surface z = 0 are T0 and ρ0 and at the upper surface z = d are Td and ρd, respectively and that a uniform temperature gradient β (=|dT/dz|) is maintained. The gravity field ![]() , a uniform vertical magnetic field
, a uniform vertical magnetic field ![]() and a uniform vertical rotation
and a uniform vertical rotation ![]() act on the system.
act on the system.
Let ![]() and
and ![]() denote the fluid velocity, pressure, density, temperature, kinematic viscosity and couple-stress viscosity, respectively. Then the momentum balance, mass balance and energy balance equations of couple-stress fluid (STOKES [7]; CHANDRASEKHAR [1]) in the presence of magnetic field and rotation are:
denote the fluid velocity, pressure, density, temperature, kinematic viscosity and couple-stress viscosity, respectively. Then the momentum balance, mass balance and energy balance equations of couple-stress fluid (STOKES [7]; CHANDRASEKHAR [1]) in the presence of magnetic field and rotation are:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The equation of state is:
| (6) |
where, ρ0, T0 are, respectively, the density and temperature of the fluid at the reference level z = 0 and a is the coefficient of thermal expansion. In writing Eq. (1), use has been made of the Boussinesq approximation, which states that the density variations are ignored in all terms in the equations of motion except the external force term. The magnetic permeability μe, thermal diffusivity χ and electrical resistivity η are all assumed to be constants.
The steady solution is:
| (7) |
Let ![]() denote, respectively the perturbations in velocity
denote, respectively the perturbations in velocity ![]() (initially zero), pressure p, density ρ, temperature T and the magnetic field
(initially zero), pressure p, density ρ, temperature T and the magnetic field ![]() . The change in density δρ, caused by the perturbation θ in temperature, is given by:
. The change in density δρ, caused by the perturbation θ in temperature, is given by:
i.e.:
| (8) |
Then the linearized perturbation equations for the couple-stress fluid are:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Within the framework of Boussinesq approximation, Eq. 9-13, becomes:
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Where:
stand for the z-components of vorticity and current density, respectively.
DISPERSION RELATION
Decompose the disturbances into normal modes and assume that the perturbed quantities are of the form:
| (19) |
where, kx, ky are the wave numbers along x- and y- directions, respectively, ![]() is the resultant wave number and n is the growth rate which is, in general, a complex constant.
is the resultant wave number and n is the growth rate which is, in general, a complex constant.
Using expression (19), Eq. 14-18 in non-dimensional form transform to:
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where, we have introduced new co-ordinates:
in new units of length d and D = d/dz'. For convenience, the dashes are dropped hereafter. Also we have put a = kd:
is the Prandtl number and:
is the magnetic Prandtl number.
Here, we consider the case where both the boundaries are free as well as perfect conductors of heat, while the adjoining medium is also perfectly conducting. The case of two free boundaries is slightly artificial, except in stellar atmospheres (Spiegel, 1965) and in certain geophysical situations where it is most appropriate. However, the case of two free boundaries allows us to obtain analytical solution without affecting the essential features of the problem. The appropriate boundary conditions, with respect to which Eq. 20-24 must be solved are:
| (25) |
DX = 0, K = 0 on a perfectly conducting boundary.
Using the above boundary conditions, it can be shown that all the even order derivatives of W must vanish for z = 0 and z = 1 and hence the proper solution of W characterizing the lowest mode is:
| (26) |
where W0 is a constant.
Eliminating Θ, K, Z and X between Eq. 20-24 and substituting Eq. 26 in the resultant equation, we obtain the dispersion relation:
 | (27) |
Where:
stand for the Rayleigh-number, the Chandrasekhar number, the Taylor number, respectively and we have also put:
and ![]() .
.
THE STATIONARY CONVECTION
When the instability sets in as stationary convection, the marginal state will be characterized by σ = 0. Putting σ = 0, the dispersion relation Eq. 27 reduces to:
| (28) |
In the absence of couple-stress parameter, rotation and magnetic field, Eq. 28 reduces to:
a result given by Chandrasekhar (1981), similarly, in the absence of couple-stress parameter and magnetic field, Eq. 28 reduces to:
a result given by Chandrasekhar (1981), in the absence of couple-stress parameter and rotation, Eq. 28 reduces to:
a result given by Chandrasekhar (1981).
To study the effects of magnetic field, couple-stress parameter and rotation, we examine the natures of:
analytically.
Equation 28 yields:
| (29) |
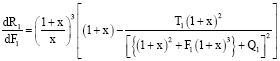 | (30) |
| (31) |
It is evident from Eq. 29 and 30 that, for a stationary convection:
may be positive as well as negative, thus, the magnetic field and the couple-stress parameter have both stabilizing and destabilizing effects on the system. It is also clear from Eq. 31 that, for a stationary convection, ![]() is always positive, thus, the rotation has a stabilizing effect on the system.
is always positive, thus, the rotation has a stabilizing effect on the system.
The dispersion relation (28) is analysed numerically. In Fig. 1, R1 is plotted against Q1 for fixed values of T1 = 100, F1 = 10 and wave numbers x = 0.5, 1.0. It depicts both the stabilizing and d e stabilizing effect o f the magnetic field on the system. Figure 2, shows the variation of R1 with respect to F1, for fixed values of Q1 = 100, T1 = 100 and wave numbers x = 0.5, 1.0. It clearly depicts both the stabilizing and destabilizing effect of the couple-stress parameter on the system. Figure 3, shows the variation of R1 with respect to T1, for fixed values of F1= 10, Q1 = 100 and wave numbers x = 0.2, 1.0.
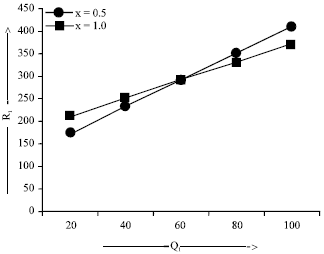 | |
| Fig. 1: | The variation of Rayleigh number R1 with Q1 for T1=100, F1 = 10, x = 0.5 and 1.0 |
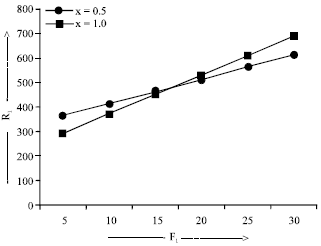 | |
| Fig. 2: | The variation of Rayleigh number R1 with F1 for Q1=100, T1 = 100, x = 0.5 and 1.0 |
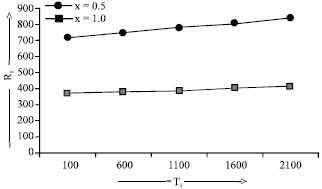 | |
| Fig. 3: | The variation of Rayleigh number R1 with T1 for F1=10, Q1 = 100, x = 0.2 and 1.0 |
The Rayleigh number R1 increases with increase in rotation parameter T1 showing its stabilizing effect on the system.
STABILITY OF THE SYSTEM AND OSCILLATORY MODES
Here we examine the possibility of oscillatory modes, on a stability problem due to the presence of rotation and magnetic field. Multiplying Eq. 20 by W*, the complex conjugate of W and using Eq. 21-24 together with the boundary conditions (25), we obtain:
| (32) |
Where:
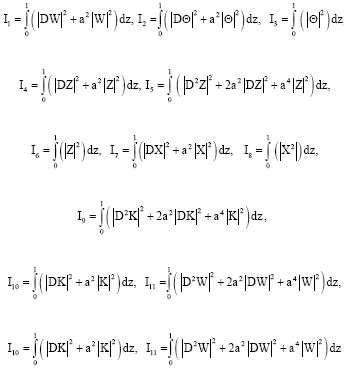 | (33) |
and σ* is the complex conjugate of σ. The integrals I1,……I12 are all positive definite. Putting σ = σr+ iσi, where σr, σi are real and equating the real and imaginary parts of Eq. 32, we obtain:
 | (34) |
| (35) |
It is evident from Eq. 34 that σr is either positive or negative. The system is, therefore, either stable or unstable. It is clear from Eq. 35 that σi may be either zero or non-zero, meaning that the modes may be either non-oscillatory or oscillatory. In the absence of rotation and magnetic field, Eq. 35 reduces to:
| (36) |
and the terms in brackets are positive definite. Thus, σi = 0, which means that oscillatory modes are not allowed and the principle of exchange of stabilities is satisfied for the couple-stress fluid heated from below. Thus, the magnetic field and rotation introduces oscillatory modes (as σi may not be zero) in the system which were non-existent in their absence.
Couple-stress fluid is an important and useful non-Newtonian fluid. Keeping in mind the importance of non-Newtonian fluids, the present paper considered the thermal convection in couple-stress fluid in the presence of uniform vertical magnetic field and uniform rotation. For stationary convection, rotation is found to have a stabilizing effect whereas the magnetic field and couple-stress have both stabilizing and destabilizing effects. The rotation and magnetic field brings oscillatory modes in the system, which were non-existent in their absence.