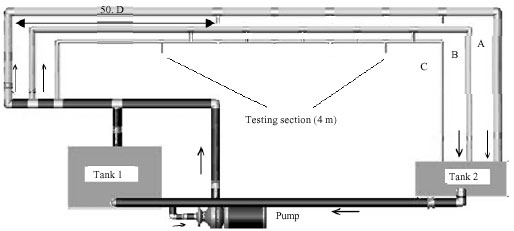
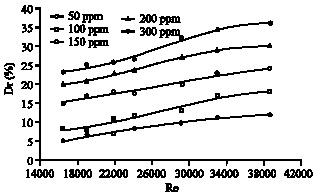
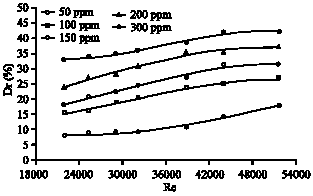
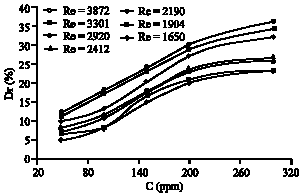
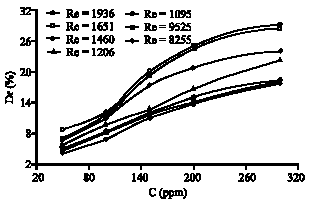
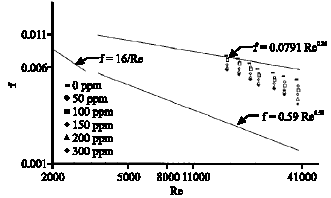
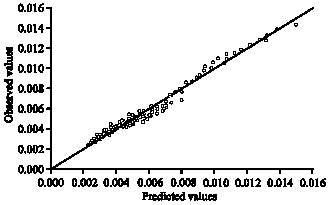
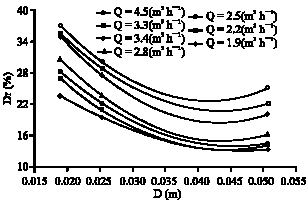Research Article
Sodium Stearate as Drag Reducing Agent in Non-Aqueous Media
Faculty of Chemical and Natural Resources Engineering, Universiti Malaysia Pahang, Kuantan, 25000, Pahang, Malaysia
R. B. Mohd. Yunus
Faculty of Chemical and Natural Resources Engineering, Universiti Malaysia Pahang, Kuantan, 25000, Pahang, Malaysia
W. K. Mahmood
Faculty of Chemical Engineering, University of Technology, Tal-Mohammed, Baghdad, Iraq
Z. B. Hassan
Faculty of Chemical and Natural Resources Engineering, Universiti Malaysia Pahang, Kuantan, 25000, Pahang, Malaysia