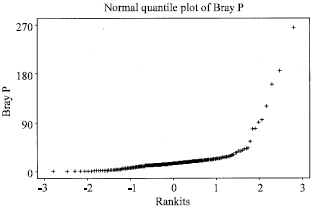
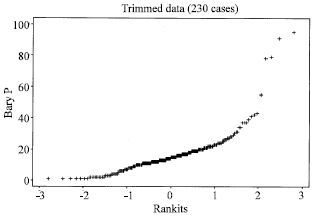
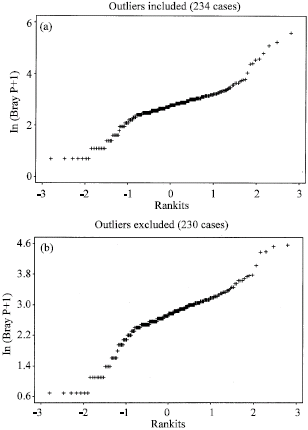
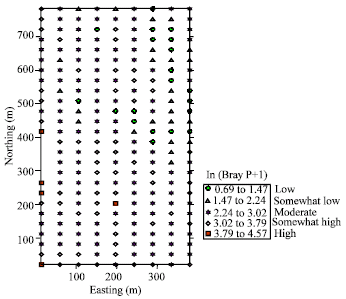
Research Article
Spatial Data Calibration for Site-Specific Phosphorus Management
Department of Agriculture Technology, Faculty of Agriculture, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
D.J. Mulla
Department of Soil, Water and Climate, Precision Agriculture Center, University of Minnesota, St. Paul, MN 55108, USA
P.C. Robert
Department of Soil, Water and Climate, Precision Agriculture Center, University of Minnesota, St. Paul, MN 55108, USA