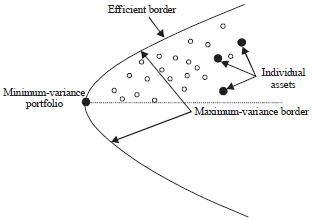
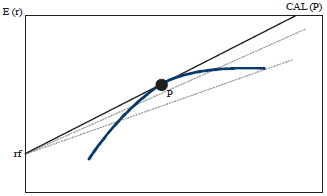
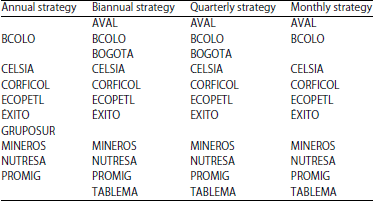
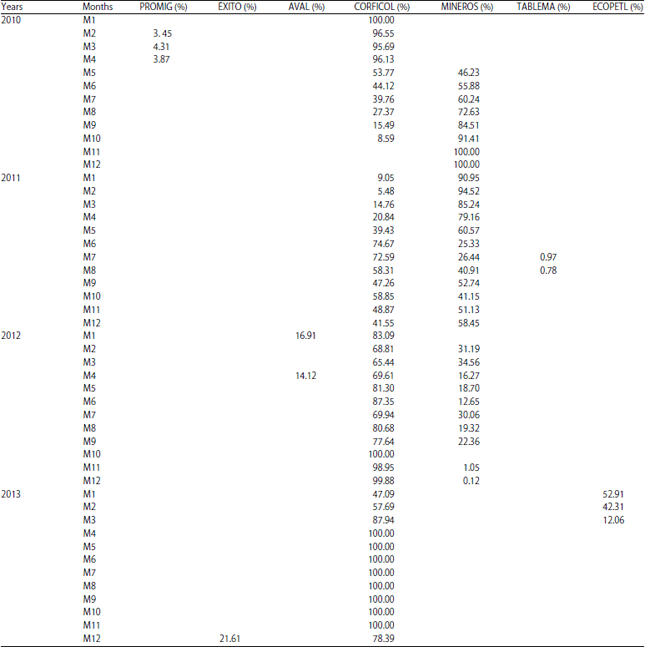
Case Study
Traditional Investment Tools Using Backtesting Simulations: The Case of Colombian Stock Market for the Period 2007-2013
School of Industrial Engineering and Business, Universidad Industrial de Santander, Bucaramanga, Colombia
Carlos E. Vecino-Arenas
School of Industrial Engineering and Business, Universidad Industrial de Santander, Bucaramanga, Colombia
Alejandra Barbosa Calderon
School of Industrial Engineering and Business, Universidad Industrial de Santander, Bucaramanga, Colombia