Research Article
GARCH Models and the Financial Crisis-A Study of the Malaysian Stock Market
Faculty of Management, Multimedia University, Cyberjaya, 63100, Malaysia
S. Wasiuzzaman
Faculty of Management, Multimedia University, Cyberjaya, 63100, Malaysia









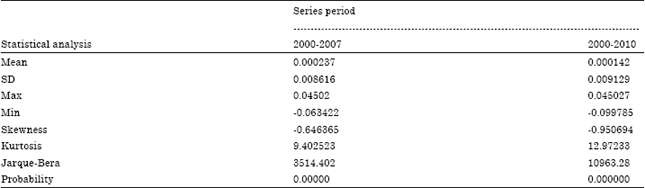




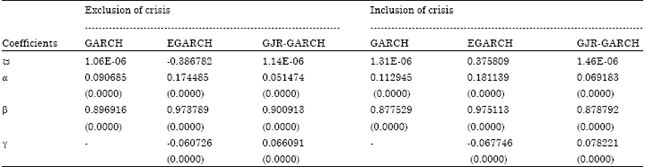
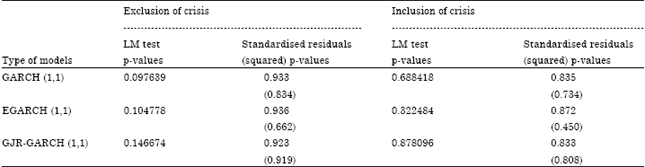


stock market malaysia Reply
I m now able to gain some of the useful information stock futures tips It will help me a lot for the initiative information.
divya Reply
Hi, I read your article and found it very interesting as well as informative. Thanks for sharing such a wonderful article with us.