ABSTRACT
In this research focus is on the estimation of the Capital Asset Pricing Model (CAPM) at different time scales for French’s stock market. The proposed methods makes possible to quantify the correlation between the return of a stock and its beta at different time scales. Our sample is composed of twenty six stocks that were actively traded over 2002-2005. The empirical results show that the relationship between the return of a stock and its beta becomes stronger as the scale increase, but the test of the linearity between the tow variables show that there is an important ambiguity. Therefore, the predictions of the CAPM are more relevant at a medium-term horizon in a multi-scale framework as compared to short time horizons.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ijaef.2007.79.87
URL: https://scialert.net/abstract/?doi=ijaef.2007.79.87
INTRODUCTION
The Capital Asset Pricing Model (CAPM) is one of the most commonly used models in asset pricing theory and practice. The CAPM, originally, proposed by Sharpe (1964) and Lintner (1965) flowing the suggestions of mean variance optimisation in Markowitz (1952), has provided a simple and compelling theory of asset market pricing for more than 20 years.
Black et al. (1972) and Fama and MacBeth (1973) were supportive the implications of the CAPM. That is, the average return of high beta stocks was higher than the average return of low beta stocks. The relationship was roughly linear, although the slope was too flat to support the CAPM strongly (Campbell, 2000).
Present research concentrate on the estimation of the CAPM at different time scale. The empirical results from different economies show that the relationship between the return of a stock and its beta becomes stronger as the scale increases. Therefore, the predictions of the CAPM are more relevant in a multi scale framework as compared to short time horizons. Then we look for the nature of the relationship between the excess return from the asset and the market premium. On other word, we test the linearity between these two variables.
The CAPM has been questioned by several empirical studies. The tests generally have found that the risk premium on individual assets can be explained by variables other than the estimated covariance. In particular, the own variance, firm size and the month of January seem to be variables that help to explain expected returns (Ross, 1978). On other hand, several theoretical extensions of the CAPM has been tested such that the after tax CAPM, the international CAPM and the International Asset Pricing Model (IAPM).
Later studies focused on the impact of return interval of betas. This research points out the importance of time scale issue. Kothari and Shanken (1995) concluded that Fama and French’s results hinge on using monthly rather than yearly returns. They argue that the use of annual returns to estimate beta helps to circumvent measurement problems caused by non-synchronous trading, seasonality in returns and trading frictions.
A nearly study by Fama (1980 and 1981) showed that the power of macroeconomic variables in explaining the stock prices increased with increasing time length, than Handa et al. (1989) provided evidence that if different beta estimates were possible for the same stock.
In the same direction, Cohen et al. (1986) shows that the beta were sensitive to returns intervals. Similarity, Handa et al. (1993) rejected the CAPM with monthly returns were used but failed to reject the CAPM, if the yearly return interval was employed. Therefore, the studies of the impact of the time scale on the beta estimation remain very important. Lynch and Zumbach (2003) similarly emphasize the importance of a multi-scale framework in the analysis of absolute price changes to accommodate the underlying heterogeneity with intraday, daily, weekly and monthly components. Therefore, a comprehensive multi-scale approach is needed to elaborate the market dynamics across time scales in which economic agents operate.
MATERIALS AND METHODS
The capital asset pricing model implies that the excess return from asset i (in excess of the risk-free asset return) should be proportional to the market premium (market return in excess of the risk-free asset return). The derivation of the CAPM equation is based upon the assumptions of risk-averse investors, frictionless markets, absence of information costs and information asymmetries, unlimited borrowing and fending at the risk-free rate and perfect divisibility and marketability of financial assets (Copeland et al., 2004).
The CAPM established that the expected return on any risky satisfy the equation:
| (1) |
Where:
| Ri | = | Return on asset I |
| rf | = | Risk-free rate |
| Rm | = | The return on the market portfolio |
and
The market risk premium is assumed by the return (E(Rm)-rf). It represents the return over the risk-free rate required by investors to hold the market portfolio. Equation (1) can be re-written to express that the risk premium on individual asset equals its beta time the market risk premium
| (2) |
In empirical finance, the usual estimator for βi is the OLS estimate from the following regression
Where, εit is white noise disturbance term.
Data set of present study consist of some stocks in the CAC 40 index between January 1, 2002 and December 30, 2005. The CAC 40 index is taken to be the corresponding market portfolio. The risk free rate of return is assumed to be the daily EURIBOR. The data source for individual stocks and the CAC 40 is the web page http://finance.yahoo.com. Stocks prices are adjusted for dividends and splits. The daily EURIBOR is taken from the base http://www.euribor.org. EURIBOR is the rate at which euro interbank term deposits within the euro zone are offered by one prime bank to another. The sample size is 1044 market days or roughly 4 years.
Present object is to study the relationship between excess return on each individual stock and the time scales of market portfolio. In particular, we estimate a linear regression of each stock excess return (Ri-rf) on each recomposed crystal j of the market portfolio (Ri-rf)j:
| (3) |
The daily return of each stock is calculated as the log price difference
Rit=log Pit-log Pit-1 |
Where:
| Pit | = | The price of asset I at day t. The market return Rmt is taken as the log difference of the CAC 40 index: |
Rit=log Ct-log Ct-1 |
Where:
| Pit | = | The index value at day t. |
During the sample period, the beta of each individual stock is calculated from the Eq. 3 for scales j = 1, 2, …, 6. In our analysis, the scale 1 is associated with 2-4 days, scale 2 with 4-8 day dynamics, scale 3 with 8-16 day dynamics, scale 4 with 16-32 day dynamics, scale 5 with 32-64 day dynamics, scale 6 with 64-128 day dynamics. Scale 6 is the highest one at which we can calculate the beta of each stock because the next one corresponds to 128-256 day dynamics (Approximately one year).
RESULTS AND DISCUSSION
Here, main focus is on estimating the CAPM at different time scales for this group of stocks regularly traded on the French market. For commodity and simplicity and before going on presenting the empirical results, there are some necessary notations, that will be firstly used viz.
ACCOR(1), ADIDAS(2), AGF(3), AIR(4), ALCATEL(5), AXA(6), BOUY(7), CARREFO(8), CREAM(9), CRECA(10), CREDIT(11), DANONNE(12), DEXIA(13), ESSILOR(14), LAFARGE(15), LVMH(16), MICHELIN(17), OREAL(18), PEUGEOT(19), RENAULT(20), SANOFI(21), SHEIDER(22), THOMSON(23), TOTAL(24), VINCI(25), VIOLIA(26), CAC40(27).
We also need to adopt the following unities:
| Table 1: | Descriptive statistics of excess returns |
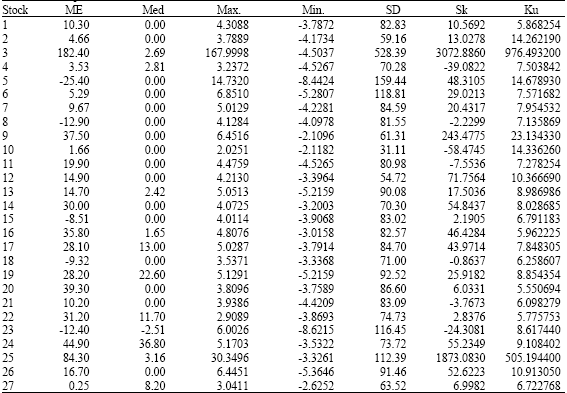 | |
Table 1 presents descriptive statistics of excess returns on the 26 stocks in the sample and on the proxy for the market portfolio, the CAC 40. The latter gathers the forty most actively-traded stocks on the French market over the past year.
Figure 1 shows that, as is the case with most financial assets, excess return on the stocks and the market portfolio exhibit little skewness but high kurtosis. It shows the recomposed crystals D1 and D6 of the excess return on the market portfolio at scale 1 and 6, respectively. D1 depicts the high frequency movements of the market portfolio, whereas D6 depicts its long-term behaviour.
Table 2 reports the OLS estimate of the regression coefficient of each stock excess return (dependant variable) versus each recomposed crystal j of the market portfolio (independent variable) versus each recomposed crystal j of the market portfolio (independent variable).
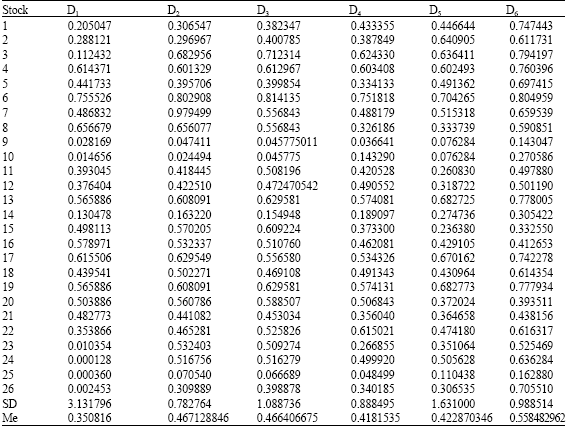
Table 3 shows that the relationship between the two variables is positive and significant at all scales. When looking at individual excess return, the mean contribution of Dim, generally, tends to decline as the scale increases and its explanatory power measured by R2 increases with the scale. This implies that the major part of the market portfolio’s influence on individual stocks is at the higher frequencies.
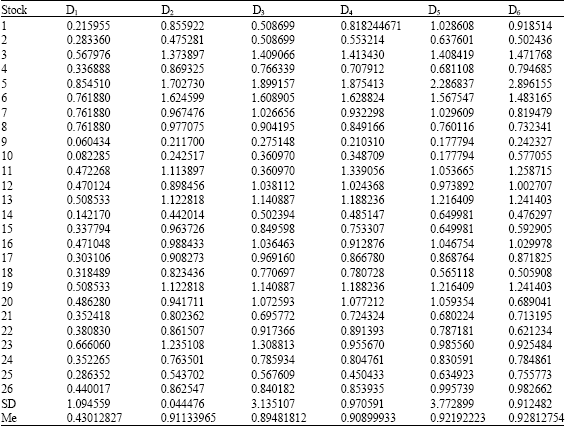
An alternative way of analysing the same issue is by regressing Eq. 3 and by changing time scales, so that scale1 will be associated with 3-6 days, scale 2 with 6-12 day dynamics, scale 3 with 12-24 day dynamics, scale 4 with 24-48 day dynamics, scale 5 with 48-96 day dynamics, scale 6 with 96-192 day dynamics. We limited at the scale 6 for the same reasons advanced above. The change of the width of the scale allows us the possibility to quantify the relation between excess return on each individual stock and the time scales of market portfolio at others scales too large as compared to scales utilized. Unlike the results reported in Table 2 and 3.
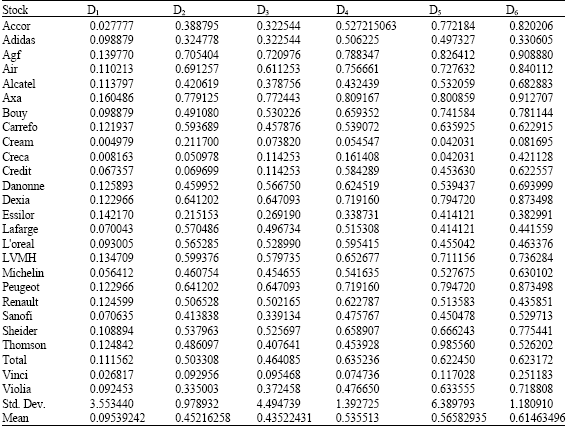
Table 4 shows that the mean contribution of Dim is concentrated at the lower frequencies. On other word, the relationship between excess return and the market portfolio becomes, in general, stronger at the higher scales of two variables (Table 5). Similar conclusions are drawn by Viviana (2005) for a sample of 24 stocks traded on the Santiago Stock Exchange.
| Table 2: | Beta for scales 1, 2, …,6 (Dyadic scales) |
 | |
| Table 3: | R2 for scales 1, 2, …,6 (Dyadic scales) |
 | |
| Table 4: | Beta for scales 1, 2, …,6 (Triadic scales) |
 | |
| Table 5: | R2 for scales 1, 2, …,6 (Triadic scales) |
 | |
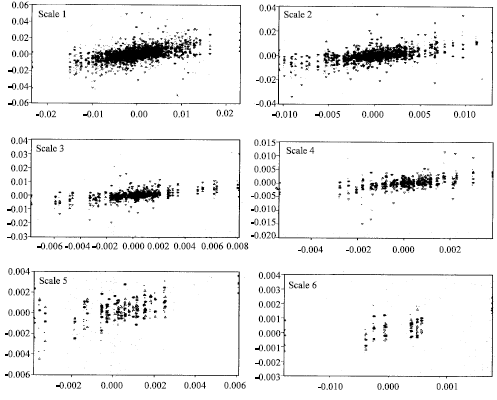 | |
| Fig. 1: | Excess return on the market (horizontal axis) against excess return on the stock (vertical axis) at different scales. Scale 1: 2-4 days, scale 2: 4-8 days and so on |
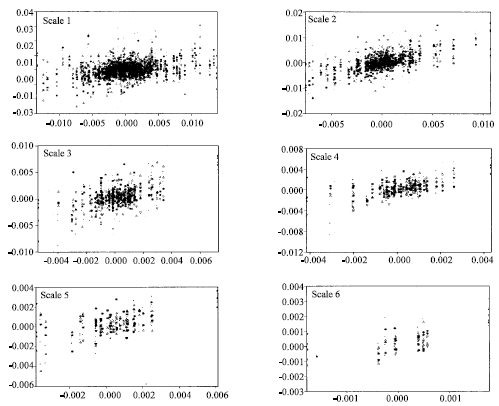 | |
| Fig. 2: | Excess return on the market (horizontal axis) against excess return on the stock (vertical axis) at different scales. Scale 1: 3-6 days, scale 2: 6-12 days and so on |
Figure 2 plots excess returns on stocks (vertical axis) against corresponding excess returns on market D1 at different scales in French stock. The scales are such that 1 is associated with 2-4 days dynamics, scale 2 is associated with 4-8 days dynamics and so on. This Fig. 2 shows that the linear association between the two variables is particularly strong at scales 2 and 3. These findings enforce the fact that the relationship between each recomposed crystal of the excess return on the stock and the corresponding recomposed crystal of the market portfolio is more relevant at the mediums scales than others scales during the sample period. Similar results are drawn by Gençay et al. (2005, 2002). Figure 2 shows that linearity between these two variables is not clear with scales more larges (scale 1: 3-6, scale 2: 6-12 and so on). So we can not conclude about the linearity between the stock return and its beta. Theses results let us to think about other methods to estimate the capital asset pricing model.
CONCLUSIONS
In this research, main focused is on the estimation of the Capital Asset Pricing Model (CAPM) at different time scales for French stock market. Our sample is composed of twenty six stocks that were actively traded over 2002-2005. The empirical results show that the relationship between the return of a stock and its beta becomes stronger at the medium scales, but the test of the linearity between the tow variables show that there is an important ambiguity. Therefore, the predictions of the CAPM are more relevant at a medium-term horizon in a multi scale framework as compared to short time horizons. We notice also that the proposed method in this paper has shown some lack in concluding about the linearity between the return and its beta (systematic risk). This leads us to think about some more adoptable and relevant methods to enlighten the ambiguity. An extension of present study using wavelet theory has been started and it seems to give good results. Wavelets are suitable adopted mathematical tools that have been world-wise developed until the 80's. They have been shown successful applications in physics, mathematics, finance, statistics, etc. We intend in the near future to obtain good results using these mathematical tools.
REFERENCES
- Fama E.F. and J.D. MacBeth, 1973. Risk Return and Equilibrium: Empirical Tests. J. Political Econ, 81: 607-636.
Direct Link - Gencay, R., F. Selcuk and B. Whitcher, 2005. Multiscale systematic risk. J. Int. Money Finance, 24: 55-70.
CrossRefDirect Link - Sharpe, W.F., 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Finance, 19: 425-442.
CrossRefDirect Link








