Research Article
Modelling the Effect of Anti-retroviral Therapy and Latent Tuberculosis Treatment in Controlling the Spread of Tuberculosis in Nigeria
Department of Mathematics and Statistics, Federal University of Technology, Minna, Nigeria
The worldwide TB epidemic is a major global health crisis. Nigeria, a country ranked 5th among the 22 high TB burden countries in the world and with the highest TB burden in Africa has a fair share of this crisis. The burden of TB in Nigeria is not precisely known but the steady rise in notification since 1995 and the relatively high case rates among adults, probably reflect a real increase in incident associated with HIV and strong transmission (Kabir, 2008).
The resurgence of Tuberculosis and other infectious diseases in the last decade has been closely linked with environmental and social changes that compromise peoples immune systems and the social structures that are used to defend against disease (Adetunde, 2009). Tuberculosis is a preventable and curable disease in almost any socioeconomic circumstances especially with the implementation of DOTS (Irajian et al., 2008). The standard treatment for active TB is Isoniazid, Rifanpicin, Pyrazinamine and Ethambutol for a period of two months followed by Isonizid and Rifampicine for a further four months. For Latent TB, the standard treatment is isoniazid alone for 6-9 months (Imam et al., 2010).
Tuberculosis is still a major global health problem and renewed interest in human tuberculosis has been stimulated due to predisposition of patients with HIV infections and multiple drug resistant strains (Gholamali and Jafar, 2009). The 59.5% of HIV patients hospitalized in University hospital in Zehedan from April 2000 to May 2005 were treated for Tuberculosis (Sharifi-Mood et al., 2006). Since the Tuberculosis epidemic in Africa has been driven by HIV, activities directed towards HIV-associated disease should logically be the most effective response. (Corbett et al., 2006).
Antiretroviral drugs are medications for the treatment of infection by retroviruses, primarily HIV. When several such drugs, typically three or four are taken in combination, the approach is known as Highly Active Antiretroviral Therapy or HAART (Dybul et al., 2002).
Antiretroviral (ARV) drugs are broadly classified by the phase of the retrovirus life-cycle that the drug inhibits. These are nucleoside reverse transcriptase inhibitors (also called NRTIs or nukes.) the non-nucleoside reverse transcriptase inhibitors, also called non-nukes or NNRTIs, the protease inhibitors or PIs, the Entry inhibitors and the Integrase inhibitor.
Antiretroviral drugs are usually used in combinations of three or more drugs from more than one class. This is called Combination Therapy. Combination therapy works better than using just one ARV drug alone. It helps prevents drug resistance.
Efforts have been made in the past to use Mathematical models to predict the effect of HIV/AIDS on Tuberculosis; this includes Porco et al. (2001) who used discrete event simulation model to predict HIVs impact on TB epidemiology. They found that HIV can significantly affect levels of TB but that the system is sensitive to the TB treatment rate. Currie et al. (2003) in a difference equation model, representing both HIV and TB dynamics with simple sub models concluded that prevention is insufficient and treatment of active TB disease should not be replaced with these measures. Cohen et al. (2006) found that current recommendations for use of single drug preventive therapy to prevent progression from infection to TB disease among those with HIV co-infection may reduce TB prevalence in the short-term but may eventually be counter-productive without directed efforts to improve the diagnosis and treatment of those with drug-resistant TB.
The objective of this study was to develop a deterministic model that will predict the effect of antiretroviral therapy and Latent TB treatment in controlling the spread of Tuberculosis.
SCHEMATIC PRESENTATION OF THE MODEL
The model equations: The Eq. 1 to 4 give the model equation for the dynamical system:
| (1) |
| (2) |
| (3) |
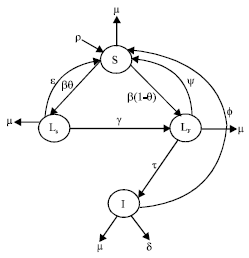 | |
| Fig. 1: | Schematic presentation of the model |
| (4) |
The model parameters and variables are given below with their respective descriptions.
S(t) is the number of Susceptible individuals at time t, LS (t) is the number of Latently infected individuals with slow progression rate to infectious class at time t, LF (t) is the number of Latently infected individuals with fast progression rate to infectious class at time t, I (t) is the number of Infectious individuals at time t, ρ is the Recruitment rate, μ is the Natural death rate. β is the Tuberculosis instantaneous incidence rate per Susceptible, θ is the proportion of infection instantaneous incidence rate with slow progression rate to infectious TB. γ is the movement rate from latent class with slow progression rate to latent class with fast progression rate. ![]() is the movement rate from latent class with fast progression rate to infectious class. δ is the Tuberculosis induced death rate ε is the recovery rate of LS ψ is the recovery rate of LF and φ is the recovery rate of I (Fig. 1).
is the movement rate from latent class with fast progression rate to infectious class. δ is the Tuberculosis induced death rate ε is the recovery rate of LS ψ is the recovery rate of LF and φ is the recovery rate of I (Fig. 1).
In this study it was assumed that there is homogeneous mixing of the population where all people are equally likely to be infected by infectious individuals in case of contact. It was also assumed for simplicity that each compartment has equal natural death rate μ. It is only at the late stage of HIV/AIDS that the immune system become weak and influences the progression from Latent class to Infectious Class. Hence early HIV-positive individuals behave in the same way as HIV-negative patients (Hughes et al., 2006).
It is important to note that in this model, it was also assumed that successfully cured individuals from Latent and infectious class becomes susceptible immediately after their treatments and could be re infected again whenever they are re exposed to TB infection irrespective of their Tuberculosis infection history. Realistically this group may enjoy some temporary immunity to tuberculosis infection and whenever they are re infected, they may require more intensive treatment as a result of some multi drug resistance that must have been built over time.
Equilibrium state of the model: The model equation were solved simultaneously and obtain the following equilibrium states. (w, x, y, z) = (ρ/μ, 0, 0, 0) as the disease free equilibrium state which is the state of complete eradication of Tuberculosis from Nigeria and
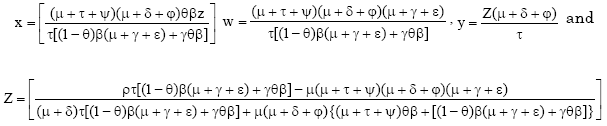 |
as the endemic equilibrium state.
The characteristic equation: The Jacobian matrix of the system equations is given by:
 |
The characteristic polynomial is obtained from the Jacobian determinant with the eigenvalues λ this gives:
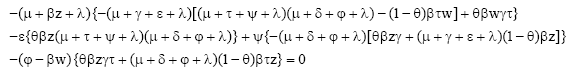 | (5) |
as the characteristic equation.
Stability analysis of the disease free equilibrium state: At the disease free equilibrium state (w, x, y, z) = (ρ/μ, 0, 0, 0) hence the characteristic equation takes the form
| (6) |
| (7) |
| (8) |
| (9) |
To establish the nature of eigenvalues in Eq. 8 We apply the result of Bellman and Cooke as applied by Sirajo (2009)
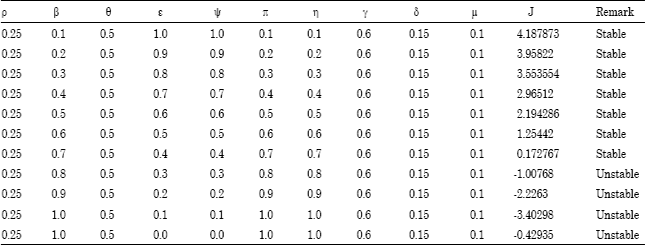
| Table 1: | Result of Stability analysis of the Disease Free Equilibrium State |
 | |
Substituting (iw) for λ and separating into real and imaginary parts, we have:
With J = F (0) G’ (0) + G (0) F’ (0)>0 using hypothetical values for the parameters with the help of a mathematical software (Maple) we obtained the Table 1.
Table 1 shows the result of stability analysis of the disease free equilibrium state . The disease free equilibrium state will be stable only when the contraction rate β is low, effective application of anti retroviral drugs thus bringing down λ, high recovery from the latent classes thus increasing ε and ψ else we will have an unstable disease free equilibrium state.
The result of this study agrees with (Imam et al., 2010) that recommends screening of every contact to an infectious TB case for Latent TB and immediate treatment of those found positive. The result also agrees with De Cock and Marston (2005) who stated that In the same way that HIV fundamentally changed Tuberculosis and its epidemiology in Africa, so the introduction of antiretroviral treatment poses important challenges on how tuberculosis control should be approached. Tuberculosis control in Africa remains weak and large gains can still be made from strengthening basic disease control. Care must be taken to avoid collapse of previously well-functioning tuberculosis control programmes after competition for scarce human resources and to ensure that integration of HIV and tuberculosis services does not compromise core tuberculosis programme functions, such as maintenance of drugs and supplies, prevention of drug resistance, assurance of quality diagnostic microscopy and cohort analysis of treated patients (Coetzee et al., 2004). The study also agrees with (Corbett et al., 2006) who stated that Without sufficient coverage of preventive and therapeutic interventions for both diseases, tuberculosis could yet be the limiting factor to the long-term success of antiretroviral programmes because of uncontrolled incidence, recurrence and institutional transmission. Currie et al. (2003) warned against replacing treatment of active TB disease with Highly Active Antiretroviral Therapy (HAART) and chemoprophylactic TB treatment (of latent infection). However, this study recommends combining the three measures for greater efficiency.
From the stability analysis carried out it became obvious that Nigeria is a stable Tuberculosis endemic nation. If Nigeria maintains the present method of Tuberculosis control (i.e., only Infectious Tuberculosis treatment) we will never be able to eradicate tuberculosis in Nigeria. The non availability of data on Latent TB treatment poses a serious threat that millions of Nigerians infected with Latent TB are out there waiting for any possible immunosuppressive condition that will break them down to Infectious TB.
The fact that TB is an air borne disease made it possible for a single infectious TB patient to infect hundreds of Susceptible individuals even before commencement of treatment thereby moving them into latent class and if these cases remained untreated, any compromise of their immune system will push them into the infectious class.