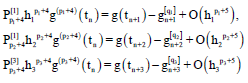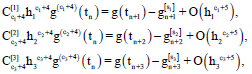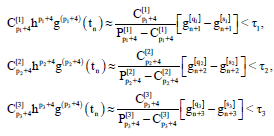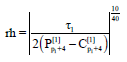Research Article
Softcode of Multi-Processing Milne’s Device for Estimating First-Order Ordinary Differential Equations
Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria
LiveDNA: 234.15858
Olaide Adetola Adesanya
Department of Mathematics, Modibbo Adama University of Technology, Yola, Nigeria
Hudson. Akewe
Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria
Hilary Izuchukwu Okagbue
Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria