Research Article
Plant Location Evaluation from the Aspects of Financial and Non-financial Criteria
Academy of Finance, No. 8, Phan Huy Chu, Hoan Kiem, Hanoi, Vietnam
LiveDNA: 84.16469
Plant location selection plays an importance role for firms in minimizing cost and retaining competitive advantages1,2. A suitable plant location is the choice that not only performs well, but also it will be flexible enough to accommodate the necessary future changes3. A poor choice of plant location might result in excessive transportation costs, a shortage of qualified labor, loss of competitive advantage, inadequate supplies of raw materials or some similar condition that would be detrimental to operations4.
For appropriate plant location selection, many financial and non-financial criteria need to be considered in decision process. These criteria include investment cost, transportation costs, nearness of facilities, availability of acquirement material, climatic conditions, access to market, availability of infrastructural facilities, availability of skilled, non-skilled labour and government influences, vv1-17. In real life, the evaluation data of plant location suitability for various subjective criteria and the weights of the criteria are usually expressed in linguistic terms. Therefore, fuzzy MCDM analysis is an optimization technique which is applied to identify the most preferred alternative under multiple criteria in vague environment1,3,15-17.
Although, numerous studies have been applied fuzzy MCDM approaches for plant location selection in literature1-17, most of them have used normal fuzzy numbers in their calculation. Lee et al.5 proposed a hybrid MCDM approach for photovoltaic solar plant location selection in Taiwan. Ray et al.2 used several MCDM methods including TOPSIS, SAW, GRA and MOORA to determine the best facility location. The ELECTRE-I method was applied to find an appropriate plant location. Mousavi et al.1 designed the integrated decision-making methodology that employs the three well-known decision-making techniques, namely Delphi, analytic hierarchical process and preference ranking organization method for enrichment evaluations (PROMETHEE) in order to make the best use of information available, either implicitly or explicitly. An application in a manufacturing company was used to demonstrate the effectiveness of their methodology. Yong15 presented a new TOPSIS approach for selecting plant location under linguistic environments, where the ratings of various alternative locations under various criteria and the weights of various criteria were assessed in linguistic terms represented by triangular fuzzy numbers. However, Chen18 indicated that that in many cases it is not to possible to restrict the membership function to the normal form and proposed the concept of generalized fuzzy numbers and their arithmetic operations. It seems that no one has developed and applied the generalized fuzzy numbers for solving the plant location selection problem.
In recent years, Technique for Order Performance by Similarity to Ideal Solution (TOPSIS)19 has been one of the well-known methods for solving MCDM problems. The fundamental idea of TOPSIS is that the chosen alternative should have the shortest distance from the positive-ideal solution and the farthest distance from the negative-ideal solution. Some recent applications can be found in20-26. In this paper, a generalized fuzzy TOPSIS approach is developed to support for plant location selection process. In the proposed approach, the ratings of alternatives and importance weights of criteria for plant location selection are represented by generalized triangular fuzzy numbers. Then, the membership functions of the final fuzzy evaluation value in the proposed approach are developed based on the linguistic expressions. Finally, this study applies the proposed generalized fuzzy TOPSIS to a case of plant location selection in a company demonstrating its advantages and applicability.
PRELIMINARIES
There are various ways of defining fuzzy numbers. In this study, the concept of fuzzy numbers is defined as follows27:
Definition 1: A real fuzzy number A is described as any fuzzy subset of the real line R with membership function fA that can be generally be defined as:
| • | fA is a continuous mapping from R to the closed interval [0, |
| • | fA (x) = 0 for all x = (-∞, a] |
| • | fA is strictly increasing on [a, b] |
| • | fA (x) = |
| • | fA is strictly decreasing on [c, d] |
| • | fA (x) = 0 for all x∈(d, ∞] |
where a, b, c and d are real numbers. Unless elsewhere specified, it is assumed that A is convex and bounded (i.e., -∞<a, d, <∞).
Definition 2: The fuzzy number A = [a, b, c, d; ![]() ] is a trapezoidal fuzzy number if its membership function is given by Dubois and Prade27:
] is a trapezoidal fuzzy number if its membership function is given by Dubois and Prade27:
 | (1) |
where, ![]() and
and ![]() are two continuous mappings from the real line R to the closed interval [0,
are two continuous mappings from the real line R to the closed interval [0, ![]() ]. From Definition 1, it is obvious that
]. From Definition 1, it is obvious that ![]() (x) the left membership function of fuzzy number A, is continuous and strictly increasing on [a, b] and
(x) the left membership function of fuzzy number A, is continuous and strictly increasing on [a, b] and ![]() (x) the right membership function of the fuzzy number A is continuous and strictly decreasing on [c, d]. If
(x) the right membership function of the fuzzy number A is continuous and strictly decreasing on [c, d]. If ![]() = 1, then A is a normal fuzzy number; otherwise, it is said to be a non-normal fuzzy number. If b≠c, A is referred to as a fuzzy interval or a flat fuzzy number. If
= 1, then A is a normal fuzzy number; otherwise, it is said to be a non-normal fuzzy number. If b≠c, A is referred to as a fuzzy interval or a flat fuzzy number. If ![]() (x) and
(x) and ![]() (x) are both linear, then A is referred to as a trapezoidal fuzzy number and is usually denoted by A = (a, b, c, d;
(x) are both linear, then A is referred to as a trapezoidal fuzzy number and is usually denoted by A = (a, b, c, d; ![]() ) or simply A = (a, b, c, d) if
) or simply A = (a, b, c, d) if ![]() = 1. In particular, when b = c the trapezoidal fuzzy number is reduced to a triangular fuzzy number and can be denoted by A = (a, b, d;
= 1. In particular, when b = c the trapezoidal fuzzy number is reduced to a triangular fuzzy number and can be denoted by A = (a, b, d; ![]() ) or A = (a, b, d) if
) or A = (a, b, d) if ![]() = 1. So, triangular fuzzy numbers are special cases of trapezoidal fuzzy numbers.
= 1. So, triangular fuzzy numbers are special cases of trapezoidal fuzzy numbers.
Definition 3: Chen18 presented arithmetical operations between generalized trapezoidal fuzzy numbers based on the extension principle.
Let, A and B are two generalized trapezoidal fuzzy numbers, i.e., A = (a1, a2, a3, a4; wA) and B = (b1, b2, b3, b4; wB) where, a1, a2, a3, b1, b2, b3 and b4 are real values, 0<wA<1 and 0<wB<1. Some arithmetic operators between the generalized fuzzy numbers A and B are defined as follows18:
| • | Generalized trapezoidal fuzzy numbers addition (+): |
| (2) |
where, a1, a2, a3, a4, b1, b2, b3 and b4 are real values.
| • | Generalized trapezoidal fuzzy numbers subtraction (-): |
| (3) |
where, a1, a2, a3, a4, b1, b2, b3 and b4 are real values.
| • | Generalized trapezoidal fuzzy numbers multiplication (x): |
where, a = Min (a1×b1, a1×b4, a4×b1, a4×b4, b = MIN (a2×b2, a2×b3, a3×b2, a3×b3), b = MIN c = Max (a2×b2, a2×b3, a3×b2, a3×b3) and d = Max (a1×b1, a1×b4, a4×b1, a4×b4).
It is obvious that if a1, a2, a3, a4, b1, b2, b3 and b4 are all positive real numbers, then:
| (4) |
| • | Generalized trapezoidal fuzzy numbers division (/): The inverse of the fuzzy number B is 1/B = (1/b4, 1/b3, 1/b2, 1/b1; wB) where, b1, b2, b3 and b4 are non-zero positive numbers or all non-zero negative real numbers. Let, a1, a2, a3, a4, b1, b2, b3 and b4 be non-zero positive real numbers. Then, the division of A and B is as follows: |
| (5) |
Definition 4
Linguistic variables and fuzzy numbers: A linguistic variable is a useful concept in dealing with situations that are excessively complex or not well-defined enough to be reasonably described in traditional quantitative expressions. These variables are values represented in words or sentences in natural or artificial languages, in which each linguistic value can be modeled by a fuzzy set Zimmermann28. The conversion scales in fuzzy set theory are applied to convert the linguistic values into fuzzy numbers. Determining the number of conversion scales is generally intuitive and subjective. The importance weights of individual criteria and the ratings of alternatives are considered linguistic variables in this study. A five-point scale is adopted to transform the linguistic values into generalized triangular fuzzy numbers. Table 1 shows the ratings and the importance weights of criteria.
| Table 1: | Generalized triangular fuzzy numbers of linguistic variables for the rating of alternatives and the importance weights of criteria |
 | |
PROPOSED APPROACH FOR PLANT LOCATION EVALUATION AND SELECTION
This section proposes a fuzzy TOPSIS method using generalized triangular fuzzy numbers for supporting the plant location evaluation and selection process.
Assume that a committee of h decision makers (Dk, k = 1,..., h) is responsible for evaluating l alternatives (At, I = 1,..., l) under n selection criteria (Cj, j = 1,..., n), where, the suitability ratings of alternatives under each of the criteria, as well as the weights of the criteria, are assessed in linguistic terms represented by generalized triangular fuzzy numbers. Criteria are classified into benefit (B) and cost (C). Benefit criterion has the characteristic of "The larger the better". The cost criterion has the characteristic of "The smaller the better". The steps of the proposed generalized fuzzy TOPSIS method are as follows:
Aggregate the importance weights: Let, wjk = (ojk, pjk, qjk, ![]() jk)), wjk∈R*, j = 1,..., n, k = 1,..., h be the weight assigned by decision maker Dk to criterion Cj. The averaged weight, wj = (oj, pj, qj), of criterion Cj assessed by the committee of l decision makers can be evaluated as:
jk)), wjk∈R*, j = 1,..., n, k = 1,..., h be the weight assigned by decision maker Dk to criterion Cj. The averaged weight, wj = (oj, pj, qj), of criterion Cj assessed by the committee of l decision makers can be evaluated as:
| (6) |
Where:
![]()
and ![]() j = min
j = min ![]() jk.
jk.
Aggregate ratings of alternative versus criteria: Let, xtjk = (atjk, btjk, ctjk; ![]() tjk), t = 1,..., l, j = 1,..., n, k = 1,..., h be the suitability rating assigned to alternative At by decision maker Dk for subjective Cj. The averaged suitability rating, xtj = (atj, btj, ctj;
tjk), t = 1,..., l, j = 1,..., n, k = 1,..., h be the suitability rating assigned to alternative At by decision maker Dk for subjective Cj. The averaged suitability rating, xtj = (atj, btj, ctj; ![]() tj) can be evaluated as:
tj) can be evaluated as:
| (7) |
Where:
![]()
and ![]() j = min
j = min ![]() tjk.
tjk.
Construct the weighted fuzzy decision matrix: Considering the different weight of each criterion, the weighted decision matrix can be computed by multiplying the importance weights of evaluation criteria and the values in the normalized fuzzy decision matrix. The weighted decision matrixes Gt are defined as:
| (8) |
Calculation of ![]() : The fuzzy positive-ideal solution (FPIS, A+) and fuzzy negative ideal solution (FNIS, A‾) are obtained as:
: The fuzzy positive-ideal solution (FPIS, A+) and fuzzy negative ideal solution (FNIS, A‾) are obtained as:
| (9) |
| (10) |
The distance of each alternative At, t = 1,..., l from A+ and A‾ is calculated as:
| (11) |
| (12) |
where, ![]() represents the shortest distance of alternative At and
represents the shortest distance of alternative At and ![]() represents the farthest distance of alternative At.
represents the farthest distance of alternative At.
Obtain the closeness coefficient: The closeness coefficient of each alternative, which is usually defined to determine the ranking order of all alternatives, is calculated as19:
| (13) |
A higher value of the closeness coefficient indicates that an alternative is closer to PIS and farther from NIS simultaneously. The closeness coefficient of each alternative is used to determine the ranking order of all alternatives and identify the best one among a set of given feasible alternatives.
APPLICATION FOR PLANT LOCATION EVALUATION AND SELECTION PROBLEM
In this section, the proposed TOPSIS method is applied for selecting and evaluating the plant location in the case of manufacturing company. Assume that the manufacturing company needs to select a location to construct a plant. Afte ran initial screening, four plant locations A1, A2, A3 and A4 are chosen for further evaluation.
| Table 2: | Aggregated weights of the criteria evaluated by decision makers |
 | |
| I: Is Important, VI: Is very important, AI: Is absolutely important | |
| Table 3: | Aggregated suitability ratings evaluated by decision makers |
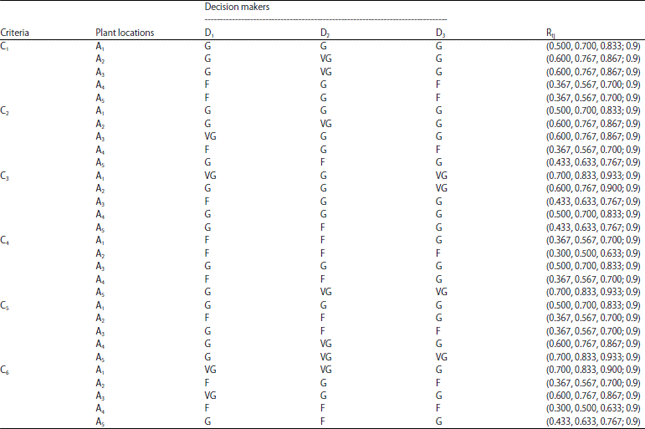 | |
| F is fair, G is good, VG is very good | |
A committee of three decision-makers, D1, D2 and D3 is formed to determine the most suitable plant location. Further assume that six criteria are selected including investment cost (C1), transportation costs (C2), availability of acquirement material (C3), access to market (C4), availability of infrastructural facilities (C5), government influences (C6).
Aggregating importance weights of criteria: Assume that the decision-makers employ the linguistic values and their corresponding generalized fuzzy numbers shown in Table 1 to evaluate the importance weights of the criteria. Table 2 displays the importance weights of six criteria from the three decision makers. Using Eq. 2-6, the aggregated weights of criteria from the decision making committee can be obtained as presented in Table 2.
Aggregate ratings of alternatives versus criteria: Three decision makers employ the linguistic rating set in Table 1 to evaluate the suitability of the plant locations under each criteria. Using Eq. 2-5 and 7, the aggregated suitability ratings of five plant locations versus each criterion from three decision makers can be obtained as shown in Table 3.
| Table 4: | Weighted ratings of each plant location |
 | |
| Table 5: | Distance of each plant location from A+ and A‾ |
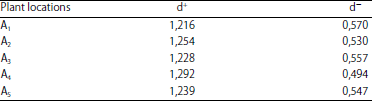 | |
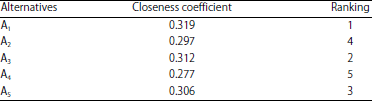
| Table 6: | Closeness coefficients of plant locations |
 | |
Determine the weighted fuzzy decision matrix: Using Eq. 2-5 and 8, the weighted fuzzy decision matrix can be obtained as in Table 4.
Calculation of ![]() : As shown in Table 5, the distance of each plant location selection from A+ and A‾ can be calculated by Eq. 9-12.
: As shown in Table 5, the distance of each plant location selection from A+ and A‾ can be calculated by Eq. 9-12.
Obtain the closeness coefficient: The closeness coefficients of plant locations can be calculated by Eq. 13, as shown in Table 6. Therefore, the ranking order of the five plant locations is A1‹A3‹A5‹A2‹A4‹. Consequently, the best plant location is A1.
Plant selection plays an importance role for all companies. Several decision makers and criteria should be involved in the decision process to select the appropriate plants. Consistent with past studies2,3, this study also concludes that most criteria for plants selection are generally evaluated by human judgment and the evaluations are subjective15. Plant selection is a highly complex and confusing problem, which may be handled effectively by intelligent systems. Therefore, plant selection can be viewed as an MCDM problem16. This study proposes a new generalized fuzzy TOPSIS approach to solve the plant location selection problem. The proposed method further extends and overcome the shortcomings of the existing fuzzy TOPSIS15-17. The proposed model allows the ratings of plants and the importance weight of criteria to be expressed in generalized triangular fuzzy numbers. The proposed method could overcome the shortcomings of existing MCDM methods for plant location evaluation4,6,12. The proposed approach and application of this study should be of interest to both companies’ managers and researchers. The results show that the proposed method is effective in plant location evaluation for the company. The proposed method may also be applied to solve other MCDM problems with similar settings in various industries such as supplier selection, distribution selection, robot selection, vv.
In this study, the generalized fuzzy TOPSIS method was developed to solve the plant location selection problem. In the proposed method the importance weights of all criteria and the ratings of various plant locations under different financial and non-financial criteria are assessed in linguistic values represented by the generalized triangular fuzzy numbers. An application of plant location selection demonstrates the computational process of the proposed model. The proposed method can also be applied to solve other MCDM problems with similar setting.
This study proposes a new TOPSIS approach using generalized fuzzy numbers to solve the plant location selection problem, where the importance weights of all criteria and the ratings of various plant locations under different financial and non-financial criteria are assessed in linguistic values represented by the generalized triangular fuzzy numbers. This study will help the companies to enhance operation efficiency and maximize their profit. The proposed generalized fuzzy TOPSIS approach can also be applied to other areas of management decision problems.
The author is very grateful to the anonymous reviewers for their insightful and constructive comments and suggestions, which have been very helpful in improving the study.