Research Article
Solving Linear Tri-level Programming Problem Using Heuristic Method Based on Bi-section Algorithm
Department of Mathematics, University of Raparin, Ranya, Kurdistan Region, Iraq
LiveDNA: 98.15322
Even to seek for the locally optimal solutions, the bi-level programming problem (BLPP) is an NP- Hard problem1,2. In fact the BLPP is an practical problem and a suitable tool for solving decision making problems. It is used in different areas such as information technology, transportation, computer science, engineering and so on. Therefore proposing the optimal solution is significant researchers.
There are different approaches to solve the BLPP3-8. These all algorithms would be divided into the following classes: Global techniques9,10, fuzzy methods11-13, meta heuristic approaches14-20, transformation methods21-27, enumeration methods28, However there is just an algorithm for solving TLPP29.
Linear bi-level and tri-level programming problems: The bi-level and tri-level programming problems would be introduced in this study.
The BLPP is defined as the following problem by Lv et al.1:
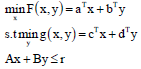 | (1) |
x,y > 0
where, ![]() and F(x, y) and g(x, y) are the objective functions of the leader and the follower, respectively.
and F(x, y) and g(x, y) are the objective functions of the leader and the follower, respectively.
Because a tri-level decision reflects the principle features of multi-level programming problems, the algorithms developed for tri-level decisions can be easily extended to multi-level programming problems which the number of levels is more than three. Hence, just tri-level programming is studied in this study.
In a TLPP, each decision entity at one level has its objective and its variables in part controlled by entities at other levels. To describe a TLPP, a basic model can be written as follows by Zhang et al.29:
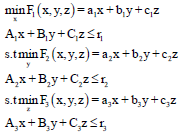 | (2) |
x,y,z > 0
where, Ai∈Rq×k, Bi∈Rq×l, Ci∈Rq×p, ri∈Rq, x∈Rk, y∈Rl, z∈Rp, ai∈Rk, bi∈Rl, ci∈Rp, i = 1, 2, 3 and the variables x, y, z are called the top-level, middle-level and bottom-level variables respectively, F1(x, y, z), F2(x, y, z), F3(x, y, z), the top-level, middle-level and bottom-level objective functions, respectively. In this problem each level has individual control variables, but also takes account of other level’s variables in its optimization function.
To obtain an optimized solution to TLP problem based on the solution concept of bi-level programming6, here first introduce some definitions and notation.
Definition 1: The feasible region of the TLP problem when i = 1, 2, 3 is:
| (3) |
On the other hand, if x be fixed, the feasible region of the follower can be explained as:
| (4) |
Based on the above assumptions, the follower rational reaction set is:
| (5) |
Where the inducible region is as follows:
| (6) |
Finally, the tri-level programming problem can be written as:
| (7) |
If there is a finite solution for the TLP problem, we define feasibility and optimality for the TLP problem as:
| (8) |
Definition 2: Every point such as is a feasible solution to tri-level problem if (x, y, z) ∈IR.
Definition 3: Every point such as (x*, y*, z*) is an optimal solution to the tri-level problem if:
| (9) |
Smooth method for TLPP: Using KKT conditions for both of last levels in problem 2, the following problem is constructed:
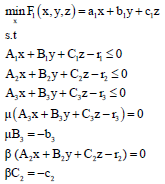 | (10) |
x,y,z,μi,βi > 0
Problem 10 is not convex and it is not differentiable. In this study, we proposed a smooth method for smoothing complementary constraints in problem 10. Using the following smooth method, problem 10 will be smoothed and then presented two algorithms based on Taylor theorem and hybrid algorithm to solve it.
Theorem 1: Let:
or:
where, m>0, n>0, then:
and:
Proof:
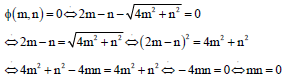 |
Also:
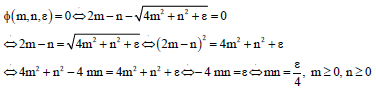 |
Using the proposed function:
in problem 10, we obtain the following problem:
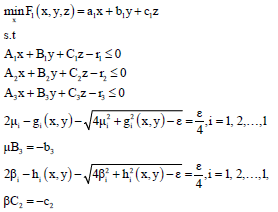 | (11) |
x,y,z,μi,βi > 0
Which in the first constraint m = μi>0, n = -gi (x, y)>0, gi (x, y) = aix+biy+ciz and ai, bi, ci are i-th row of A, B, C, respectively and in the second constraint m = βi>0, n = -hi (x, y)>0, hi (x, y) = aix+biy+ciz-r and ai, bi, ci are i-th row of A, B, C.
Let:
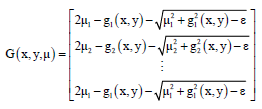 | (12) |
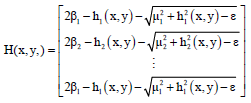 | (13) |
| (14) |
Problem 11 can be written as follows:
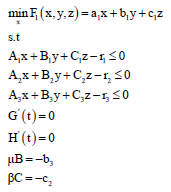 | (15) |
x,y,z,μ,β > 0
Where:
t = (x, y, μ)∈Rk+2l
Because problem 10 equal to 15, used the following method for solving problem 15.
Proposed algorithm based on bi-section method
Theoretical concepts: Nonlinear equations are difficult to solve, therefore there are many algorithms to approximate of the root these equations. Bi-section algorithm is one of the most important methods to approximate the root. Necessary condition to use this method, is the uniqueness root of the nonlinear equation. The necessary definitions and theorems have been proposed by Hosseini and Kamalabadi21.
By applying the Taylor theorem to a feasible point such as tk for functions G’ and H’ taking only two linear part of them in problem 15, the following linear functions are constructed:
| (16) |
Let:
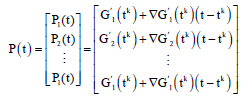 | (17) |
| (18) |
Let:
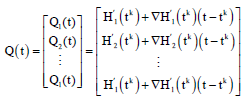 | (19) |
Using Taylor theorem for G’ and H’ at tk and 17, 19, in problem 15 obtained the following problem:
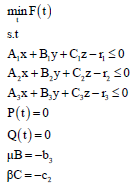 | (20) |
t, μ, β>0
Steps of the bi-section algorithm: The steps of the bi-section algorithm for f(x) = 0 as follows:
| Step 1: | Input a,b |
| Step 2: | let x = (a+b)/2:print x |
| Step 3: | If ABS(f(x))<ε then end |
| Step 4: | If f(a)f(x)<0 then let b = x else let a = x |
| Step 5: | GOTO 2 |
| Step 6: | End |
ε is a positive small number
Steps of the proposed algorithm: The steps of the proposed algorithm are as follows:
Step 1
Initialization: The feasible points a and b are created randomly and according to theorem 1, error ε is appropriate given error and finishing the algorithm depends on ε.
Step 2
Finding solution: Using in step 1 and bi-section algorithm for in problem 15, two non-linear equations P(t) = 0 and Q(t) = 0 have been solved. Let t*1, t*2 are roots of P(t) = 0 and Q(t) = 0, if t*1 = t*2 let t* = t*1 = t*2 and go to the next step else go to step 4.
Step 3
Making the present best solution: If t* solves the following problem go to the next step else go to step 1:
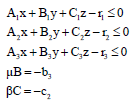 |
Step 4
Termination: If d(F(t*1), F(t*2))<ε then the algorithm is finished and:
is the best solution by the proposed algorithm. Otherwise, go to the step 1. Which d is metric and:
Following theorems show that the proposed algorithm is convergent.
Theorem 2: Every Cauchy sequence in real line and complex plan is convergent.
Proof: Proof of this theorem was given by Rudin30.
Theorem 3: Sequence {Fk} which was proposed in above algorithm is convergent to the optimal solution, so that the algorithm is convergent.
Proof: Let:
According to step 4:
| (21) |
Therefore:
There is large number such as N which k+1>k>N and j = 1, 2,…, 2m+n we have:
Therefore:
Now let m = k+1, r = k then we have:
This shows that for each fixed j, (1<j<2m+n), the sequence (Fj(1), Fj(2),…) is Cauchy of real numbers, then it converges by theorem 2.
Say, Fj(m) → Fj asm → ∞. Using these 2m+n limits, we define F = (F1, F2,…, F2m+n). From 18 and m = k+1, r = k:
d(Fm, Fr)<ε1
Now if r → ∞, by Fr → F we have d (Fm, F)<ε1.
This shows that F is the limit of (Fm) and the sequence is convergent by definition 3 therefore proof of theorem is finished.
Theorem 4: If sequence {f(tk)} is converge to f(t) and f be linear function then {tk} is converge to t.
Proof: Proof of this theorem is given by Rudin30.
Theorem 5: Problem 15 and 23 are equal therefore they have same optimal solutions.
Proof: It is sufficient we prove that, ∣G’(t)-P(t)∣<ε and ∣H’(t)-Q(t)∣<ε for every arbitrary ε>0. According to the problem 19, 20 we have:
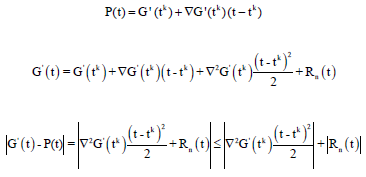 |
Now if n → ∞, from 18:
and let ∣∇2G’(tk)∣<m that m is an arbitrary large number, this is possible because ∇2G’(tk) is a number.
If k → ∞ because F is linear then by theorems 3 and 4 tk → t therefore ∣tk-t∣<ε2, say:
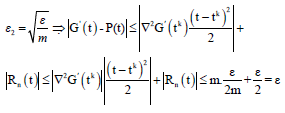 |
Now proved:
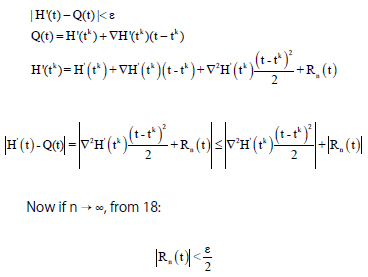 |
and let ∣∇2H’(tk)∣<m that m is an arbitrary large number, this is possible because ∇2H’(tk) is a number.
If k → ∞ because F is linear then by theorems 3 and 4 tk → t therefore ∣tk-t∣<ε2 , say:
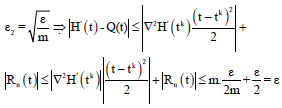
This finished proof of theorem.
Computational results: To illustrate both algorithms, considered the following examples:
Example 1: Consider the following linear tri-level programming problem by Zhang et al.29:
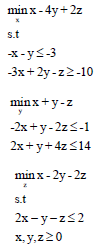 |
Using KKT conditions, the following problem is obtained:
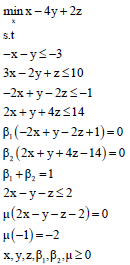 |
By the proposed function, the above problem becomes:
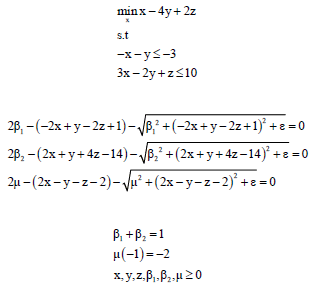 |
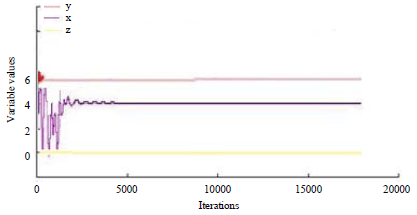 | |
| Fig. 1: | Behavior of variables with ε = 0.001 in example 1 |
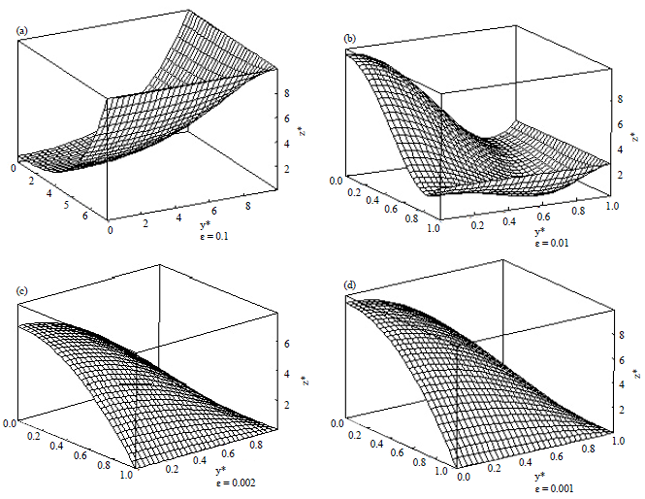 | |
| Fig. 2(a-d): | Dimensionless distribution at different axial positions, y, z, t, for fix ε in example 1 |
| Table 1: | Comparison of optimal solutions by Taylor algorithm-example 1 |
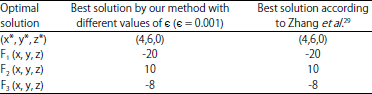 | |
Using the Taylor theorem, we obtain a problem in the form of problem 20 and solve it using the proposed algorithm. Optimal solution is presented according to Table 1. Behavior of the variables in example 1 has been show in Fig. 1. Dimensionless distribution at different axial positions has been shown in Fig. 2.
Example 2: Consider the following linear tri-level programming problem by Zhang et al.29:
| Table 2: | Comparison of optimal solutions by Taylor algorithm-example 2 |
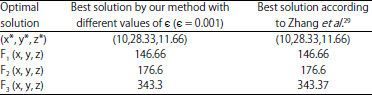 | |
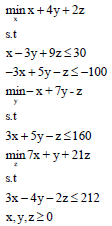 |
Optimal solution for this example is presented according to Table 2. Behavior of the variables has been showed that variables x and y will be stable after 1000 and 4000 iterations respectively.
In this study, KKT conditions were used to convert the problem into a single level problem. Then, using the proposed function, the problem was made simpler and converted to a smooth programming problem. The smoothed problem was been solved, utilizing the first proposed algorithm based on Taylor theorem. Comparing with the results of previous methods, this algorithm has better numerical results and present better solutions. The best solutions produced by proposed algorithm were feasible unlike the previous best solutions by other researchers.
In the future works, the following would be researched:
| • | Examples in larger sizes can be supplied to illustrate the efficiency of the proposed algorithms |
| • | Showing the efficiency of the proposed algorithms for solving other kinds of TLP such as quadratic and non-linear TLP |
The author would like to extend his thanks to the Faculty of Mathematics, University of Raparin. Special thanks also for Quality Assurance of the university which supported this study.
This study discovers an approach for solving the tri-level programming problem which is efficient not only for tri-level but also other kinds of multi-level programming problems. An efficient and feasible method based on bi-section algorithm is presented in this study. Most of the previous studies for BLPP have used approximate method which has high complexity order and has not efficient solution. The heuristic proposed algorithm in this study is based on an exact method which has never been proposed before. This study will help the researchers to solve other NP-Hard problems of optimization area.