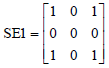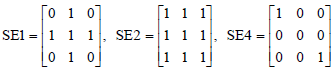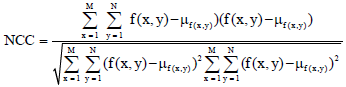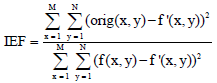Research Article
A Case Study of Impulse Noise Reduction Using Morphological Image Processing with Structuring Elements
Department of ECE, SEEE, SASTRA University, Thanjavur, Tamil Nadu, India
Har Narayan Upadhyay
Department of ECE, SEEE, SASTRA University, Thanjavur, Tamil Nadu, India
K. Narasimhan
Department of ECE, SEEE, SASTRA University, Thanjavur, Tamil Nadu, India
J. Jezebel Priestley
Department of ECE, SEEE, SASTRA University, Thanjavur, Tamil Nadu, India