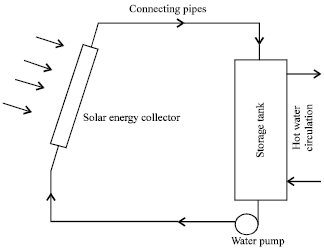
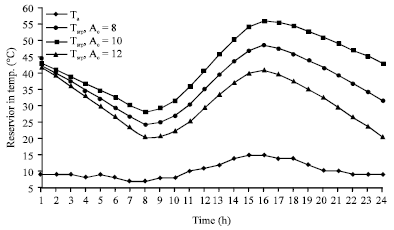
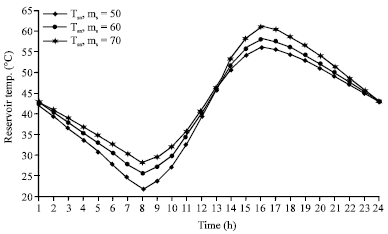
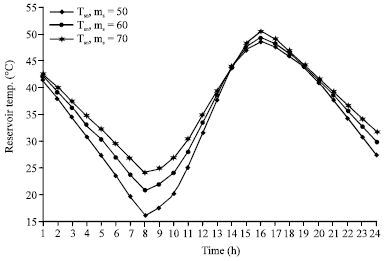
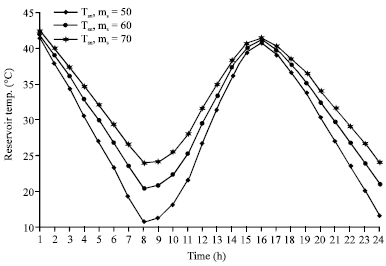
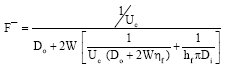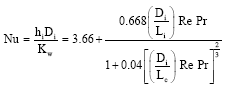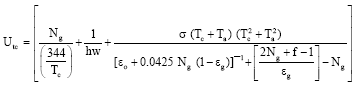Research Article
Analytical Analysis of Thermal Energy Storage Performance of Room Heating System by Solar Energy
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Hussain H. Al-Kayiem
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Maki H. Khalaf
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Nassir D. Dhamin
Department of Mechanical Engineering, College of Engineering, University of Tikrit, Iraq