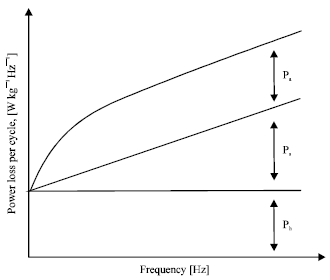
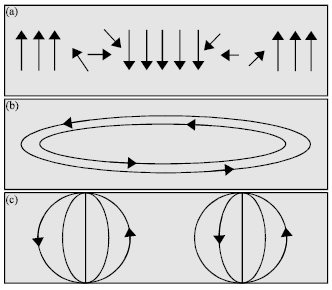
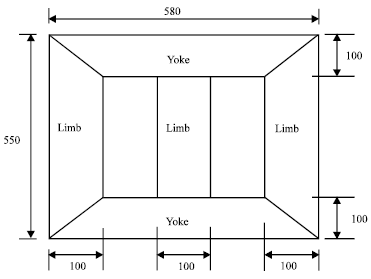
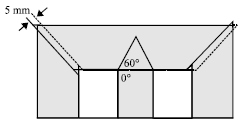
Research Article
Analyze Eddy Current Loss in the Three Phase 100 kVA Transformer Core with the Mix 60°-0° T-joint Core
School of Electrical System Engineering, Universiti Malaysia Perlis (UniMAP), P.O. Box 77, d/a Pejabat Pos Besar, 01007 Kangar Perlis, Malaysia