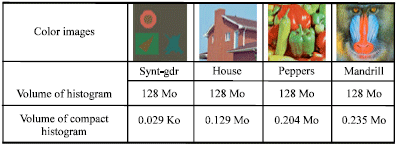
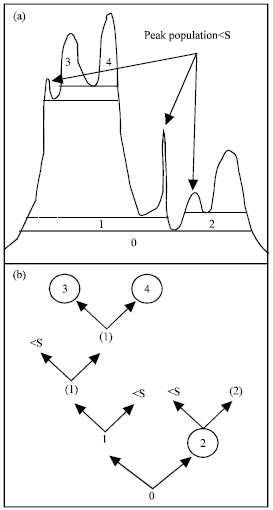
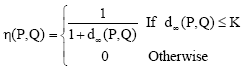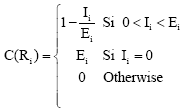Research Article
Full 3D Compact Histogram Segmentation of Color Images
Laboratoire d`Instrumentation, d`Image et de Spectroscopie (L2IS), Institut National Polytechnique Felix Houphouet-Boigny, BP 1093, Yamoussoukro, Cote d`Ivoire
A. Clement
Laboratoire d`Ingenierie des Systemes Automatises (LISA), Institut Universitaire de Technologie, BP 42018, 49016 ANGERS CEDEX, France
B. Vigouroux
Laboratoire d`Ingenierie des Systemes Automatises (LISA), Institut Universitaire de Technologie, BP 42018, 49016 ANGERS CEDEX, France