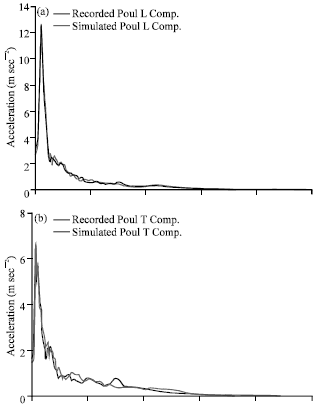
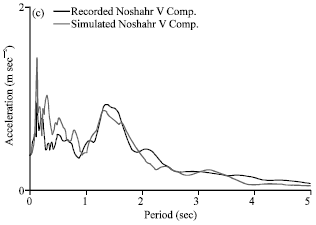
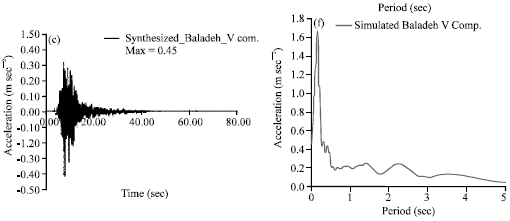
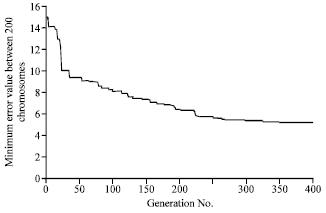
Research Article
Synthesizing the 2004 Mw 6.2 Kojour Earthquake Using Empirical Green’s Function
Department of Civil Engineering, Iran University of Science and Technology, Tehran, Iran
R. Abbasnia
Department of Civil Engineering, Iran University of Science and Technology, Tehran, Iran
M. Bozorgnasab
Department of Civil Engineering, Iran University of Science and Technology, Tehran, Iran
Y. Eslamian
Department of Civil Engineering, Iran University of Science and Technology, Tehran, Iran