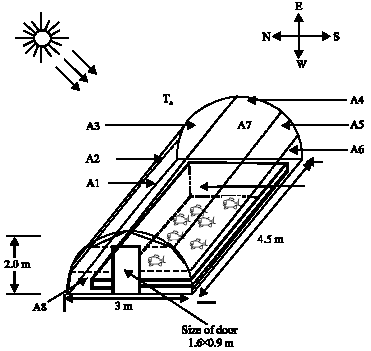
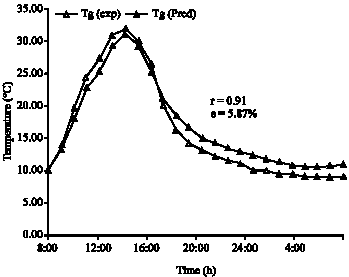
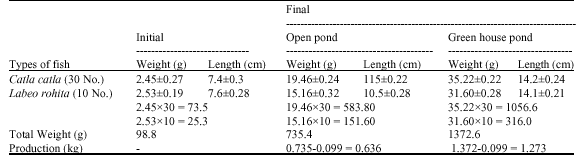
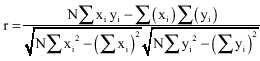Research Article
Modeling the Thermal Performance of Solar Heated Fish Pond: An Experimental Validation
Centre for Energy Studies, Indian Institute of Technology Delhi Hauz Khas,New Delhi-110016, India
G.N. Tiwari
Centre for Energy Studies, Indian Institute of Technology Delhi Hauz Khas,New Delhi-110016, India
Tribeni Das
Centre for Energy Studies, Indian Institute of Technology Delhi Hauz Khas,New Delhi-110016, India
Bikash Sarkar
Central Institute of Freshwater Aquaculture (Indian Council of Agricultural Research) Kausalyaganga, Bhubaneswar-751002, India