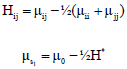Research Article
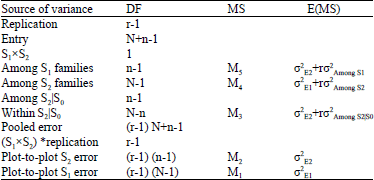
Estimation of Genetic Parameters of Selfing Population Derived from an Equilibrium One I. Theory
Assessment Institute for Agricultural Technology of Central Kalimantan (BPTP Kalimantan Tengah), Jl. G. Obos Km. 5, Palangka Raya, Kalimantan Tengah, 73112, Indonesia
Nasrullah
Faculty of Agriculture, Gadjah Mada University, Jl. Flora Bulaksumur, Yogyakarta, Indonesia
Woerjono Mangoendijojo
Faculty of Agriculture, Gadjah Mada University, Jl. Flora Bulaksumur, Yogyakarta, Indonesia
Panjisakti Basunanda
Faculty of Agriculture, Gadjah Mada University, Jl. Flora Bulaksumur, Yogyakarta, Indonesia