Research Article
Redistribution of Water Injected into the Soil
Not Available
Zahra Izadpanah
Not Available
Seyed A.A. Jafari Moosavi
Not Available
Sap flows between soil layers of different moisture content (termed hydraulic redistribution) have the potential to influence water budgets and species interaction (Peek et al., 2005). Using a great deal of excremental data, Brooks and Corey, (1966) showed that the relationship between water content θ and capillary pressure (h) and between hydraulic conductivity (k) and capillary pressure (h) can be expressed by
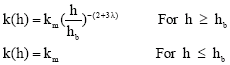 | (1) |
And
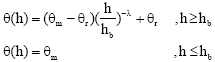 | (2) |
In these equations, θm is the maximum volumetric water content, km is the corresponding hydraulic conductivity, λ is a dimentionless exponent, hb is the displacement suction (bubbling pressure head) and θr is the residual water content. Mahmoodian-Shooshtari et al. (1984) investigated the parameters in the Brooks and Corey (1966) k(h) and h(θ) relationships analytically and experimentally. The method is based upon fitting an analytically derived response function to the corresponding measured one for one dimensional vertical redistribution of water injected into the soil. The theoretical response function used is:
| | (3) |
where
h0 (t) = Capillary pressure head at r = 0, t = time
| | (4) |
θ1 = Initial water content
hb, λ, θm and km are defined as before and
V = volume of injected water per unit area.
Equation 3, which was derived from Richards’ Equation by neglecting gravity forces, assumes that k and θ are single valued function of h. It was also necessary to use an assumed distribution of water content to derive Eq. 3. The water content distribution was approximated by a series of step functions (Spiegel, 1999).
This study presents a theoretical h0(t) solution for radial redistribution of water injected into the soil and then compared with the Eq. 3. The reasons for investigating radial redistribution was to ascertain if there are any inherent advantages to this geometry.
Richard’s equation: Richards’ equation for radial flow without gravity effect is:
| | (5) |
Where r is the radial coordinate in a horizontal plane. Two boundry conditions and one initial condition are required to obtain solution. There are no exact solution available for this equation, but approximate analytical and numerical solutions have been developed by various investigators. Regardless of the method selected for solution, realistic data or mathematical expressions are needed for k(h) and θ (h).
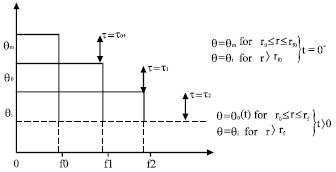
Radial redistribution: The flow phenomenon under consideration is the radial redistribution of a slug of water that is rapidly injected on the cylindrical surface (r = r0) into a semi infinite soil with uniform initial water content. Figure 1 shows a homogeneous soil thinckness b with uniform initial water content θ1, which is situated between two horizontal impervious boundaries having a central bore of radius ro. A known volume of water, say V, is injected instantaneously into the soil through the openings of the bore walls. Immediately after injection of water, the moisture begins to move outward from the moist shell under the influence of capillary-pressure gradients. The boundary conditions for this model are:
| | (6) |
Which means no water flux at ![]()
The initial conditions are described by
| | (7) |
And
| | (8) |
Also, continuity requires that
| | (9) |
The coordinate of the wetting front at t = 0 (rfo) is
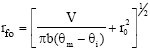 | (10) |
Theoretical response function for radial redistribution: Integrating Eq. 5 over r, from r0 to r, subject to boundary condition (6), gives
| | (11) |
It is assumed that the distribution of water content at any stage during the flow process is given by the step function (Spiegel, 1999) (Fig. 2) distribution which is
| | (12) |
Where rf is the coordinate of the wetting front and θ0 is the water content at r = r0. Substituting for θ from Eq. 12 into the right hand side of Eq. 11 carrying out the indicated integration gives
| | (13) |
Again, integrating both sides of the results with respect to r over the interval and r0 ≤ r≤ rf yields
 | |
| Fig. 1: | Schematic diagram of physical model for radial redistribution |
 | |
| Fig. 2: | Step function for moisture distribution |
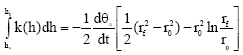 | (14) |
On the other hand, for Eq. 12 and 9 requires that
 | (15) |
Introducing rf from Eq. 15 into Eq. 14 yields
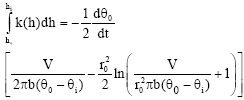 | (16) |
In terms of capillary pressure head h0 at r = 0, Eq. 2 becomes
| | (17) |
And, thus
 | (18) |
Also,
 | (19) |
Substituting Eq. 1, 19 and 17 into Eq. 16 for k(h),![]() and θ0, respectively and performing the required operations with θI = θr yields
and θ0, respectively and performing the required operations with θI = θr yields
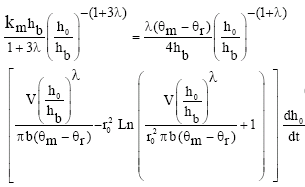 | (20) |
Letting ![]() separating variables, integrating over time from 0 to t and over
separating variables, integrating over time from 0 to t and over ![]() Eq. 20 becomes.
Eq. 20 becomes.
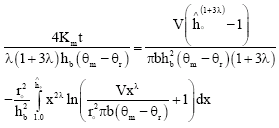 | (21) |
Defining
| | (22) |
and
| | (23) |
Eq. 21 in dimensionless form is
| | (24) |
Effect of λ and ![]() on theoretical curves for radial redistribution: To demonstrate the influence of each of the parameters λ and
on theoretical curves for radial redistribution: To demonstrate the influence of each of the parameters λ and ![]() on the theoretical response, h0(t) was calculated from Eq. 24 using three different values of each parameter with the other parameter held constant. The results of these computations are shown is Fig. 3 and 4 where
on the theoretical response, h0(t) was calculated from Eq. 24 using three different values of each parameter with the other parameter held constant. The results of these computations are shown is Fig. 3 and 4 where ![]() is plotted as a function of
is plotted as a function of ![]() .
.
The information shown in Fig. 3 indicates that the shape (slope) of the ![]() (t) curves is dependent on the values of λ. Figure 3 also shows that the effect of λ becomes less pronounced as λ increases. The difference in the slope for λ = 1.5 and λ = 2.25 is greater than the difference between λ = 2.25 and λ = 3.0. Support is given for this observation by the fact that the permeability reduced tremendously with small increases in capillary-pressure head for a porous medium of high λ value.
(t) curves is dependent on the values of λ. Figure 3 also shows that the effect of λ becomes less pronounced as λ increases. The difference in the slope for λ = 1.5 and λ = 2.25 is greater than the difference between λ = 2.25 and λ = 3.0. Support is given for this observation by the fact that the permeability reduced tremendously with small increases in capillary-pressure head for a porous medium of high λ value.
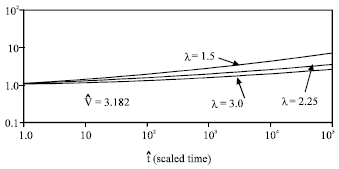 | |
| Fig. 3: | Compartion of radial solutions (theoretical) for different values of λ with other parameters held constant |
 | |
| Fig. 4: | Compartion of radial solutions (theoretical) for different values of |
Indeed, the saturated voids of a medium with high λ value empty suddenly when the capillary pressure head reaches a value somewhat greater than hb, after which the moisture redistribution is greatly slowed due to the rapid drop in permeability associated with the small increase of capillary-pressure head above hb. Figure 4 indicates that the shape and vertical location of the curves are also influenced slightly by ![]() . Because
. Because ![]() is a function of V, r0, b, θm and θr the change indicated in the curves is due to variations in any one, or a combination of these parameters.
is a function of V, r0, b, θm and θr the change indicated in the curves is due to variations in any one, or a combination of these parameters.
Comparisons of solutions to Eq. 3 and 21: As mentioned before, the purpose of developing the radial response function h0(t) was to investigate the possible advantages inherent in the radial redistribution over the vertical one. Therefore a comparison of the vertical and radial response function h0(t) is given here. Using Eq. 3 and 21 and the parameter values in Table 1, two solutions to the h0(t) function were obtained. These solutions are shown in Fig. 5 the values of the integral in Eq. 21 were obtained numerically using the Simpson’s rule of integration.
| Table 1: | Values of parameters used in Eq. 3 and 21 for calculation of time (Mahmoodian Shooshtari, 1982) |
 | |
| * Assuming θi = θr in Eq. 4 | |
 | |
| Fig. 5: | Compartion of vertical and radial solutions to the moisture redistribution process |
Figure 5 shows that, for the same soil parameters and volume of injected water, radial redistribution occur at a faster rate than one dimensional redistribution. This is to be expected, since for the radial case the moisture redistribution is multi- directional rather than in one direction for the vertical case.
The slight advantage that is gained by more rapid redistribution for the radial case is more than offset by other disadvantages, however. For example, Eq. 22 must be evaluated by numerical integration while Eq. 3 is an analytical closed from solution. The advantage of an analytical solution over a numerical solution for the purposes of matching calculated and measured response function is obvious. However, the authors suspect that repeated numerical solutions to Eq. 21, coupled with a search procedure, would be required to determine the values of parameters given the minimum different between measured and calculated h0(t) relationships. As it is apparent the form of Eq. 3 greatly facilitates computation of the parameter values. Furthermore, the flow process for the radial case is not as simple to initiate and monitor experimentally as is the vertical case.
The function h0(t) is the most easily measured response variable at the soil surface. Except for a slightly more rapid redistribution, no advantages for radial redistribution over the vertical one were observed.