Genetic Analysis of Kernel Size and Kernel Weight in Bread Wheat (T. aestivum L.)

MATERIALS AND METHODS

This study was conducted during cropping season of 1997-98 and 1998-99 at the experimental field of Cukurova University, Faculty of Agriculture, Department of Field Crops, Adana, Turkey. This region has typical Mediterranean climatic  conditions with an average annual rainfall of 700-750 mm for long term. The experiments were carried out under rainfed conditions.

Three bread wheat genotypes 84 CZT 04 (large-kerneled), Panda (medium-kerneled) and Bow”S”/Crow”S” (small-kerneled) was chosen on the basis of their kernel weight differences, were used as parents in this study.

Crossing procedure: The six basic generations (P_1, P₂, F₁, F₂, BC₁ and BC₂) were derived from three bread wheat reciprocal crosses at the end of 1997-98 growing season.

During the 1998-99 crop season, parents, F₁, F₂, BC₁ and BC₂ generations were sown in a randomized complete-block design with three replications, each containing 40 experimental rows as follows:

Ten kernels were sown by hand in each 1 m row with a plant to plant distance of 10 cm. The rows were spaced 30 cm apart. Data were collected on each plant basis for the following characters.

Large kernel ratio (%): Determined from the total weight of grain harvested from each plant using grain sizer which have 2.8 mm openings. All kernels of each plant sifted and plump kernels are those which remained on top of sieve and thin kernels are those which pass through 2.8 mm openings both were collected and weighed and data expressed in percent.

1000 kernel weight (g) : The mean weight in grams of 3x100 randomly selected kernels expressed as 1000 kernel weight.

Variance analysis test applied according to Randomized Completely Block Design (RCBD) (Steel and Torrie, 1980). Mean comparisons of the generations within each cross were made by using Duncan's Multiple Range Test (DMRT) for each character.

Genetic parameters: Heterosis was calculated as the percentage increase of F₁ performance, above the mean parental performance:

Inbreeding depression was expressed as the percent reduction of the F₂ mean below performance:

Heritability: Generation variances were partitioned into additive (V_D), dominance (V_H) and environmental (V_E) components as outlined by Mather and Jinks (1971).

Narrow sense heritability estimated using Warner (1952) equation:

Joint scaling test and six parameter model: In the joint scaling test, means of the six generations were used to estimate mean (m), additive (d) and dominance (h) effects for each characters in each cross by the method as described by Mather and Jinks (1971). These estimates were then used to obtain the expected values of the six generations. Observed and expected means were compared to test the validity of the model and significance control made using χ² test.

Since the additive-dominance model was inadequate to explain genetic architecture for researched plant characters, then six parameter model fitted to generation means to indicate genetical components, using methods outlined by Hayman (1958), Singh and Chaudhary (1985). Significance of the parameters was tested against their corresponding standard errors.

For the computing joint scaling test and six-parameter model values, Microsoft Excel Computer Software was used.

RESULTS

Parental and generation means (Table 1) were significantly different for large kernel ratio in all crosses. F₁ generation mean was closed to the greater parent in Panda X 84 CZT 04, 84 CZT 04 X Bow”S”/Crow”S”, 84 CZT 04 X Panda, Bow”S”/Crow”S” X Panda and Bow”S”/Crow”S” X 84 CZT 04, whereas generation mean of F₁ for Panda X Bow”S”/Crow”S” was higher than that of the greater parent.

The F₂ mean was generally lower than the F₁'s except Bow”S”/Crow”S” X 84 CZT 04 cross. The backross means were tended to be intermediate between the F₁ and recurrent parent. These data suggest that large kernel ratio is dominant over low.

Generation means were significantly different for 1000 kernel weight in all crosses. These differences between parental genotypes for kernel weight was chief aim of this study. F₁ generation means were more or less closer or higher than that of greater parental genotypes for the trait as above said. These results showed that dominance and additive effects were consistent and important for kernel weight.

Table 1:	Means and variances for large kernel ratio and 1000 kernel weight of three bread wheat and their reciprocal crosses
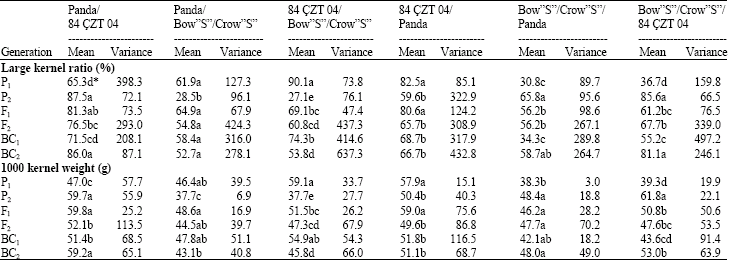*Means followed by the same letter are not significantly different based on Duncan's New Multiple Range Test (p = 0.05)

Table 2:	Genetic parameters for large kernel ratio and 1000 kernel weight of three bread wheat and their reciprocal crosses
Genetic parameters for large kernel ratio and 1000 kernel weight of three bread wheat and their reciprocal crosses

Table 3:	Joint scaling test and six-parameter results for large kernel ratio and 1000 kernel weight of three bread wheat and their reciprocal crosses
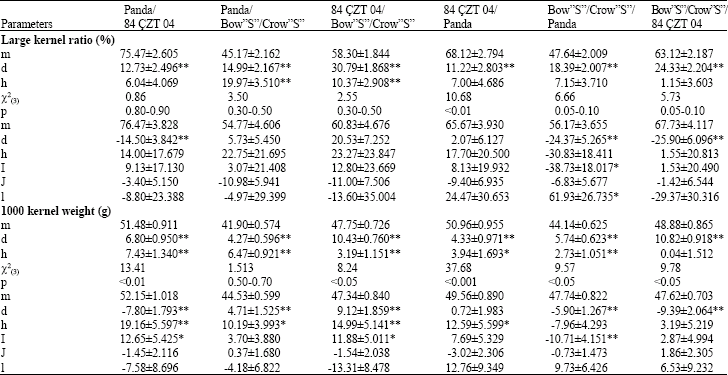For the six-parameter model (i): Stands additive x additive, (j): Additive x dominance, (l) Dominance x dominance epistatic gene effects; *Significant; **Highly significant

Heterosis, inbreeding depression and heritability: Different heterotic values were detected for the large kernel ratio (Table 2). The percentage of heterosis over the mid-parents, ranged from 6.37 to 43.53% according to crosses. Higher narrow sense heritability calculated in Panda x 84 ÇZT 04 and Panda x Bow”S”/Crow”S” crosses were 99.0 and 60.0%, respectively. Unrealistic (very low narrow sense heritability) values obtained for other crosses.

Estimates of heterosis ranged from 0.63 to 15.42% for 1000-kernel weight for the crosses. Higher heterotic effect was obtained for all crosses except Bow”S”/Crow”S” X 84 CZT 04. Higher inbreeding depression found in all crosses except Bow”S”/Crow”S” X Panda. Higher narrow sense heritability was obtained for Panda X 84 CZT 04 and Bow”S”/Crow”S” X Panda crosses as 82 and 100%, respectively. While narrow sense heritability obtained for 84 CZT 04 X Bow”S”/Crow”S” was moderate.

The joint scaling test and six-parameter model: For the large kernel ratio, significant additive gene effect was found in all crosses, while in Panda x Bow”S”/Crow”S” and 84 CZT 04 x Bow”S”/Crow”S” crosses dominance gene effect was significant (Table 3), Significant additive x additive (l) and dominance x dominance (l) epistatic gene actions was detected in Bow”S”/Crow”S” x Panda cross for the large kernel ratio.

Significant additive and dominance gene effect detected in all crosses according to joint scaling test for 1000-kernel weight. Significant additive x additive (i) epistatic effect was known in three combinations.

DISCUSSION

This study was arranged to investigate genetical architecture of grain size and grain weight in bread wheat. To estimate genetic parameters and gene action types; generation means and the joint scaling test (based on three and six-parameter model) were used. Scaling, the joint scaling (based on a three-parameter model) and estimates of the additive, dominance and interactive effects (based on six-parameter model) were useful to indicate genetical mechanism of some plant characters and many researchers used this methods for inheritance studies (Esparza and Foster, 1998; Zhang et al., 1999; Przulj and Mladenov, 1999; Malik et al., 1999; Sharma et al., 2002; Akhtar and Chowdhry, 2006).

The findings of this research showed that; differences for large kernel ratio and 1000 kernel weight between six basic generation (P₁, P₂, F₁, F₂, BC₁ and BC₂) means were significant which indicates that these characters were heritable. High narrow-sense heritability estimates for some crosses in present study is supporting these results. Higher heritability was pointed by several researchers for grain size (Esparza and Foster, 1998) and grain weight (Ketata et al., 1976; Novoselovic et al., 2004).

Estimates of three and six-parameters showed that additive-dominance model was adequate for large kernel ratio in all crosses exception of 84 CZT 04/Panda. Additive effects were main factor affecting the large kernel ratio. So early generation selection for this character should be effective for wheat breeding programs. These results are in accordance with the previous findings of Esparza and Foster (1998). However, for 1000-kernel weight, additive-dominance model was inadequate for five out of six cross combinations except Panda/Bow”S”/Crow”S”. Epistatic gene actions are important expression of this character in addition to additive-dominant gene effects. Therefore for this character, selection should be relatively slow and continuous for next generations. In a range of studies related to inheritance of 1000-kernel weight over dominance and dominance x dominance effects were noticed (Kashif and Khalig, 2003; Akhtar and Chowdhry, 2006). Shamsuddin and Rahman (1998) indicated that kernel weight was controlled by additive, dominance and epistatic gene action.

For the large kernel ratio and kernel weight, maternal effect may be important because of the different hetrosis values according to reciprocal crosses. Higher heterosis was detected in the crosses where large kerneled parent used as female. These results suggested that to increase kernel size or weight, parental genotype with large-kerneled should be used as female. For an efficient breeding program, choosing the suitable parent is very important for the researched plant trait. Maternal effects, the contributions of the mother to her offspring above and beyond the equal parental genetic contributions are expected to be substantial in seeds. Genetic maternal effects are potentially considerable because the seed coat is genotypically maternal and the endosperm has a larger maternal than paternal nuclear contribution (Platenkamp et al., 1993). Kearsey and Pooni (1996) and Akhtar and Chowdhry (2006) pointed out that different parent can also effect the phenotype of their progeny either directly or indirectly that was called as maternal effect.

ACKNOWLEDGMENT

This manuscript includes a part of Ph.D study which was financial supported by the Cukurova University, Research Fund.