ABSTRACT
In this study nine statistical models were tested to determine sugarbeet yield response to nitrogen (N) fertilizer application. Statistical analysis indicated that the best model fitted to the data was quadratic model according to different criteria (suitability of the Law of Diminishing Returns, coefficient of determination and standard error of the estimate). In addition, N fertilizer applied by farmers was compared with the amount of fertilizer suggested by experts. It was found out that sugarbeet farms used less (73.99 kg ha-1) and excess (68.91 kg ha-1) N fertilizer. This leaded to loss of yield and money.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ajps.2004.529.531
URL: https://scialert.net/abstract/?doi=ajps.2004.529.531
INTRODUCTION
Fertilization and other agronomic applications are essential to get high yield and quality of product in agriculture[1]. As a result of many studies, it has been determined that balanced fertilizer use leads to over 50% yield increase in agricultural production under suitable conditions. However, non-appropriate (excess, less or unconscious) fertilizer applications may lead to yield decrease, loss of farmer’s income, loss of foreign exchange of the country and environmental problems[2]. Therefore, determination of technical (physical), economic and ecologic optimum levels of fertilizer application is very important.
Production function is an important tool in the explanation of input-output relationships[3-6]. Directly or indirectly, decisions concerning optimal rates of fertilizer involve fitting a model to yield data where several rates of fertilizer have been tested. Although several different models are commonly used to describe crop yield response to fertilizers, it is seldom explained why one model is selected over others[7,8]. Obviously, fertilizer recommendation should be derived using the most appropriate model. Agronomist and agricultural economists have spent more than a century in search of such a model[9]. Several different response models have been used to identify economic optimum rates of nitrogen (N) fertilization and many researchers have noted that these models often disagree when identifying these rates[5,7,10-13].
The aim of this study was to compare and evaluate different statistical models describing the response of sugarbeet to N fertilizer application. In addition, economic loss or gain of farmers is determined using chosen model.
MATERIALS AND METHODS
Literature review shows that many studies have relate on research station experimental data. These data fit the model well. However, farm conditions are not the same as experimental conditions. Therefore, it is worthwhile to evaluate data obtained from farms[14]. Cross-section data on sugar beet yield and fertilizer use were collected by formally interviewing 75 farmers in the central county of Tokat province, Turkey. Data belong to the production period of 2002-2003. In addition, farmers’ N fertilizer application was compared with the data of Research Institute of Tokat.
Models: In the simplest form, an observed yield function can be written as:
where, Y is yield, W is weather variables, S is soil type variables, N is total supply of nutrients (N = SN+X); where, SN is soil nutrients; X is fertilizer application, G is genetic factor, O is other factors[15]. This general form was then simplified for practical use since it is not possible to test all variables under farm conditions. The simplified function is:
where, Xi is fertilizer application and Xj is all other constant factors.
To describe the sugarbeet yield response to N fertilizer, nine statistical models[16] were fitted to the data using Minitab Release 12.1.
Selection criteria for the best model: In the selection of the best model, suitability of model to the “Law of Diminishing Returns” is very important.
In most previous studies, empirical models have generally been judged only on the bases of coefficient of determination (R2). It was generally accepted that the greater the level of fit, the better the model. This criterion was explicitly followed by numerous researches. However, some researches say that R2 on its own does not provide sufficient support for selecting any one model over another. Therefore, other criteria (i.e. standard error), in addition to this, should be used for choosing the appropriate specification[14].
This study assumes that N fertilizer costs are the only variable costs and that all other costs are fixed. To compute the level of fertilizer application at technical optimum, first derivative of function according to input (fertilizer) is taken and equated to zero. For the calculation of the level of fertilizer application at economic optimum, the Nop was calculated by setting the first derivative of the N fertilizer response curve equal to the ratio between the cost of fertilizer and the price of crop. That is: dy / dx = Px / Py, where, Px is price per unit of input (fertilizer), Py is price per unit of output (sugarbeet). In the study the cost of N fertilizer and the price of sugarbeet were used as $0,03476 and $0,05825 kg-1, respectively.
In the determination of farms, which use fertilizer less or excess, economic optimum level of fertilizer suggested by Research Institute (±%10) is taken consideration.
RESULTS AND DISCUSSION
The coefficients of determination for the models varied, the lowest 0.105 and the highest 0.151. In all models R2 is low because there are other factors (irrigation, high yield seed, mechanization, etc.) affecting crop yield.
According to coefficient of determination (R2) and standard error of estimate (SE), quadratic model was chosen to calculate economic optimum level of N fertilizer use because results were in favour of this model (Table 1). Optimum fertilizer rates were calculated, given the input-output price ratios.
Quadratic function is as follows:
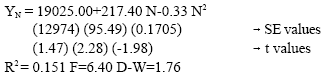 |
Estimated coefficients were of the expected sign and were also all statistically significant at the 1% level.
The difference between N fertilizer application of farmers and suggested amount by experts is 26.84 kg ha-1 at technical optimum level and 27.40 kg ha-1 at economic optimum level (Table 2). This result is similar to the findings of another study conducted on the same region in the production period of 1999-2000. The researchers determined that sugarbeet producers applied 307.40 kg ha-1 at technical and 301.50 kg ha-1 N fertilizer at economic optimum level [17].
Research findings indicated that 37.33% of farms (28 out of 75 farms) used less, but 17.33% (13 out of 75 farms) more fertilizer than the amount suggested by Research Institute. It was determined that some of the farmers used 73.99 kg ha-1 less fertilizer and as a result loss of yield was 8032.70 kg ha-1 for farms which used less N fertilizer than suggested amount. On the other hand, the amount of excess N fertilizer application was 68.91 kg ha-1 for farms, which used more fertilizer than suggested level. For this farms yield loss was calculated as 5099.58 kg ha-1. The amount of loss of money for farms that used both less and excess N fertilizer for sugarbeet was $465.33 and $299.45 ha-1 (Table 3).
| Table 1: | Functional relationships between sugarbeet yield and nitrogen use |
 | |
| Logarithmic figures | |
| Table 2: | Comparison of the farmer’s fertilizer application and yield level with technical and economic optimum (kg ha-1) |
| Table 3: | Comparison of nitrogen fertilizer use (less or excess) in sugarbeet production |
 | |
To sum up, quadratic model is best suited to describe yield response of sugarbeet to N fertilizer according to selection criteria. It was observed that some of the sugarbeet producers in the region used fertilizer non-appropriately. This leaded to yield and financial loses. As far as environmental problems caused by unconscious N fertilizer application are concerned, determination of ecological optimum levels of N fertilizer application is needed.
REFERENCES
- Belanger, G., J.R. Walsh, J.E. Richards, P.H. Milburn and N. Ziadi, 2000. Comparison of three statistical models describing potato yield response to nitrogen fertilizer. Agron. J., 92: 902-908.
Direct Link








