Research Article
Genetic Analysis of Some Yield Contributing and Quality Characters in Spring Wheat (Triticum aestivum)
Not Available
N.A. Siddquie
Not Available
M.Robiul Alam
Not Available
A.S.M.M.R. Khan
Not Available
M.S. Alam
Not Available
Wheat (Triticum aestivum) is the second most important cereals in Bangladesh next to rice. In terms of food value wheat is more nutritious than rice. Wheat grain supplies carbohydrate, protein, minerals and certain vitamins (BARI, 1990). The yield potentiality of the varieties cultivated in Bangladesh is much less than cultivars of the developed countries. Information on genetic control of yield and yield components is very much helpful in designing a breeding programme (Shamsuddin and Abi - Antoun, 1986). For a sound breeding programme a plant breeder needs to be aware of the relative importance of different gene actions involved in the inheritance of concerned characters (Bhadra and Aparna, 1985). Regression of Wr (parents-offspring covariance) on Vr (array variance) and its graphical presentation provides some information on gene action, when certain assumptions, such as diploid segregation, absence of epistasis, independent gene distribution, etc. as listed by Hayman (1954) are met. In order to get a clear picture of the genetic situation the present investigation was under taken using seven diverse spring wheat varieties.
Seven varieties of spring wheat (Triticum aestivum) Sonalika, Gaurab, Saurav, Mayoor, Aghrani, Pavan and Chyria-3 were crossed in all possible combination excluding reciprocals. The 21 F1s and the seven parents were grown in a randomized complete block design (RCBD) with three replications at the field laboratory of the Department of Genetics and Plant Breeding, Bangladesh Agricultural University, Mymensingh, during rabi season of 2000-2001. Each genotype was grown in a single row plot of 1.5 m long in each replication. The seeds were sown keeping the she space 25 cm between the rows and 5 cm between the plants of the same row. Observation on seven yield contributing and a quality characters viz., days to maturity, plant height, spikes per plant, spike length , grains per spike, 1000-grains weight and grain yield per plant were recorded on 10 random plants excluding border ones. Protein content was determined in the laboratory by multiplying the total nitrogen content. Total nitrogen was determined by Micro-Kjeldahl method. They were analyzed for wr/vr graph of Jinks (1954) and Hayman (1954).
The Vr/Wr analysis for days to maturity gave a regression coefficient (b), which was significantly different from zero (Fig. 1). This supports the adequacy of additive dominance model in explaining genetic situation for this character. On the other hand, plant height, spikes per plant, spike length, grains per spike, 1000-grains weight, grain yield per plant and protein content showed insignificant regression coefficients from zero (Fig. 2–8). This indicates the evidence of epistasis for these characters. By comparing (Vr+Wr) with Yr (parental mean), we could see the direction of dominant alleles.
Days to maturity: Vr/Wr graph for days to maturity indicates that simple additive dominance genetic model to be adequate without complicacy of non allelic interaction for maturity.
 | |||
| Fig. 1: | Vr/Wr graph for days to maturity | ||
| A = Sonalika, | B = Gourab, | C = Sourav | |
| D = Mayoor, | E = Aghrani, | F = Payon | |
| G = Chyria-3 | |||
 | |
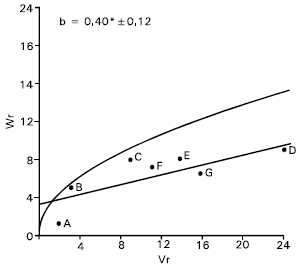
| Fig. 2: | Vr/Wr graph for plant height |
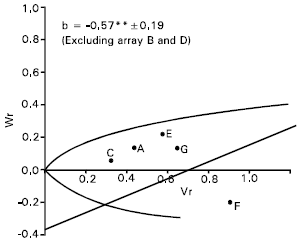 | |
| Fig. 3: | Vr/Wr graph for spikes per plant |
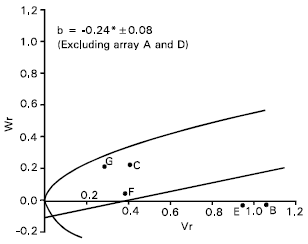 | |
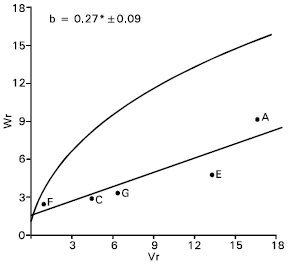
| Fig. 4: | Vr/Wr graph for spike length |
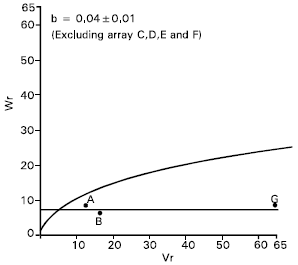 | |
| Fig. 5: | Vr/Wr graph for grains per spike |
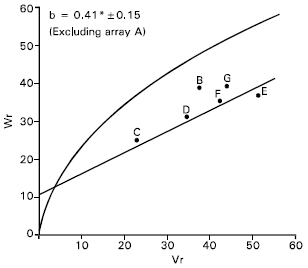 | |
| Fig. 6: | Vr/Wr graph for 1000-grain weight |
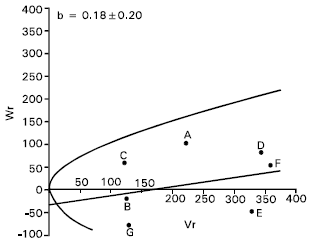 | |
| Fig. 7: | Vr/Wr graph for grain yield per plant |
 | |||
| Fig. 8: | Vr/Wr graph for content protein | ||
| A = Sonalika, | B = Gourab, | C = Sourav | |
| D = Mayoor, | E = Aghrani, | F = Payon | |
| G = Chyria-3 | |||
There was an indication of partial dominance, because the regression line cut the Wr axis above the origin (Fig. 1), and took the position very close to the limiting parabola. The distribution of the parents along the regression line showed that the parent Sonalika (A) took the position very close to the origin. This indicates that Sonalika (A) contained most of the dominant alleles. Whereas the parent Mayoor (D) took distant position from the origin suggesting that recessive alleles were concentrated in this parent. The rest of the parent fell between these two as follows: ABCFEGD. The array positions of the other parents suggest that they contained both recessive and dominant genes.
The correlation coefficient has been estimated between Yr and (Vr+Wr) and it was positively significant (r = 0.92, P<0.05). This indicates the dominant alleles in the parent were responsible for early maturity. Additive and dominance gene effects for maturity time spring wheat were reported by Dhanda and Sethi (1996). Khalifa et al. (1997) reported partial dominance for early maturity.
Plant height: There was an evidence of epistasis in case of plant height as the regression slope (b = 0.16±0.17) was non significant from zero (Fig. 2). By excluding two arrays in turn from the analysis attempt was made to trace out the interacting arrays (Hayman, 1954) for the character. It was noticed that none of the arrays excluding except Gourab (B) and Mayoor (D) could make any real improvement of the slope. With the parent Gourab and Mayoor excluded from the analysis the regression slope (b = 0.40±0.12) was significantly different from zero at P<0.05, indicating additive dominance model adequate for the character. Vr/Wr graph for plant height (after excluding array of Gourab and Mayoor) there was an indication of partial dominance, because the regression line intersected the Wr axis above the origin (Fig. 2). Distributing of the parents along the regression line showed that the parent pavon (F) took the position very close to the origin. This indicates that Pavon (F) contained most of the dominant alleles. Whereas the parent Sonalika (A) took the position from the origin suggesting that recessive alleles were concentrated in this parent. The other parents took their position intermediate between these two parents, and indicating that they contained both dominant and recessive alleles.
The correlation coefficient has been estimated between Yr and (Vr+Wr), it was positive but non significant (r=0.24). This indicates that dominant alleles in the parents were not responsible for increasing plant height.
Both additive and non additive gene actions for the character were also reported by many investigators (Shamsuddin et al., 1993; Aglodiya and Shukla, 1994; Rajara and Maheshwari, 1996). Amawate and Behl (1995) reported additive dominance gene effect for plant height.
Spikes per plant: The regression slope (b = - 0.06±0.40) was not significantly different from zero for spikes per plant (Fig. 3). This indicate additive dominance model as inadequate for the character. By omitting two arrays Gourab (B) and Mayoor (D) from the analysis, the regression slope (b = -0.57±0.19) was significantly different from zero at (P<0.05) indicating additive dominance model was adequate for the character. This suggests that the parent Gourab and Mayoor conferred interacting alleles to the offspring when they were crossed with other parent.
The regression line cut the Wr axis below the origin and took the position away to the limiting parabola (Fig. 3). This suggests that, the character was controlled by over dominance type of gene action. Distribution of the parents along the regression line showed that the parent Sourav © took the position close to the origin, indicating that the parent contained most of the dominant alleles for this character. Whereas the parent Pavon (F) took the distant position from the origin, suggesting that it contained the largest number of recessive alleles. Rest of the parents took intermediate position between these two parents. The correlation between Yr and (Vr + Wr) was positive and significant (r = 0.91). This indicates that dominant alleles in the parents were responsible for decreasing spikes per plant. Lonc (1988) reported partial dominance for this character. Varma and Yunus (1986) observed additive dominance gene action for spikes per plant but Shamsuddin and Abi-Antoun (1986) reported over dominance for this character.
Spike length: Epistasis was evident for spike length as the regression slope (b = 0.08±0.13) is non significant from zero (Fig. 4). By excluding two arrays Sonalika (A) and Mayoor (D) from the analysis, the regression slope (b = -0.24±0.08) was significantly different from zero at P<0.05 indicating additive dominance model was adequate for the character. This suggests that the parent Sonalika (A) and Mayoor (D) contained the epistatic alleles for spike length.
The regression line suggests (Fig. 4) that the character was controlled by over dominance gene action. Distribution of the parents along the regression line showed that the parent Chyria-3 (G) contained the larger proportion of dominant alleles. Whereas the parent Gourab (B) had the most recessive alleles and consequently took the distant position from the origin. The non significant correlation coefficient (r = 0.64) was obtained between the parental mean Yr and (Vr + Wr). This suggests the direction of dominance was ambiguous. Lonc (1988) reported partial dominance for spike length. Chowdhry et al. (1999) observed this character was controlled by partial dominance. But Walia et al. (1994) reported additive and dominance gene action for spike length.
Grains per spike: Epistasis was also showed by the character grains per spike as the regression slope (b = -0.12±0.31) was not significantly different from zero. By excluding four arrays, Sourav, (C), Mayoor (D), Aghrani (E) and Pavon (F) from the analysis, the regression slope, (b = 0.04±0.01) became significantly different from zero at P<0.05 (Fig. 5). This suggests that the parents Sourav, Mayoor, Aghrani and Pavon contained the epistatic alleles for grains per spike .
After excluding arrays C, D, E and F from the analysis it was noticed that simple additive model was adequate for the character. Dominance may be considered partial because the regression line cut Wr axis above the origin (Fig. 5). The parent Sonalika (A) contained the larger proportion of dominant alleles. On the other hand the parent Mayoor (G) had the most recessive alleles and consequently took the distant position from the origin.
The correlation coefficient between parental measurement (Yr) and parental order of dominance (Vr + Wr) was non significant (r = 0.44) indicating that direction of dominance was ambiguous. Shamsuddin and Abi-Antoun (1988) reported partial dominance for this character and epistatic gene action. Rajara and Maheshwari (1996) and Patil and Bhavsar (1997) reported non additive gene action for this trait.
1000-grains weight: Vr/Wr graph for 1000-grains weight indicated an evidence of epistasis as the regression slope (b = 0.37±0.20) was non significant from zero. By excluding single array Sonalika (A) from the analysis, the regression slope (b = 0.42±0.15) was significantly different from zero at P<0.05 indicating adequacy of additive dominance model for the character (Fig. 6).
The regression line (Fig. 6) indicates that the character was predominantly controlled by additive gene action. Distribution of the parents along the regression line showed that the parent Sourav © contained most of the dominant alleles whereas recessive alleles were contained by the parent Aghrani (E) for the character. The other parents were between these two alleles, indicating that they contained both dominant and recessive alleles.
The correlation value between Yr and (Vr+Wr) was negatively non significant (r = -0.04) indicating that direction of dominance was ambiguous.
Shamsuddin and Abi-Antoun (1986) reported partial dominance under space planting condition, but under solid seeding condition they observed complete dominance. Shamsuddin and Rahman (1998) reported that 100-grains weight was controlled by additive, dominance and all other types of epistasis. Rajara and Maheshwari (1996) reported predominance of non additive gene action for 1000-grain weight. On the other hand Chowdhry et al. (1999) reported over dominance for this character.
Grain yield per plant: For grain yield per plant there is evidence of epistasis as the regression coefficient (b = 0.18±0.20) was not significantly different from zero (Fig. 7). By excluding four arrays ABCD, BCDE, CDEF and DEFG consecutively from the analysis, the regression slope did not significantly different from zero. This suggests that there was non allelic interaction among the parents for this character. Therefore, the additive dominance model is not adequate for this character. The yield contributing characters spikes per plant, spike length, grains per spike and 1000-grains weight had epistatic gene action, which might have caused non additiveness to grain yield.
It was also reported that grain yield per plant was controlled by both additive and non additive gene action (Aglodiya and Shukla, 1994; Rajara and Moheshwari, 1996 Patil and Bhavsar, 1997). Shamsuddin et al. (1993) and Atale and Vitkare (1990) also reported that grain yield per plant was predominantly controlled by non additive gene action.
Protein content: The analysis of Vr/Wr graph showed regression coefficient (b = 0.07±0.18) was not significantly different from zero. This indicate additive dominance model was inadequate for the character. By omitting two arrays Mayoor (D) and Pavon (F) from the analysis, the regression slope (b = 0.57±0.19) was significantly different from zero at P<0.05 indicating additive dominance model was adequate for the character (Fig. 8). This suggest that the parent Mayoor and Pavon conferred interacting alleles to the offspring when they were crossed with other parents.
The regression line cut the Wr axis above the origin and took the position very close to the limiting parabola (Fig. 8). This suggests that the character was controlled by predominantly additive gene action. Distribution of the parents along the regression line showed that the parent Sonalika (A) took the position close to the origin. This indicates that the parent contained most of the dominant alleles for this character. Whereas the parent Aghrani (E) took distant position from the origin, suggesting that the recessive alleles were contained by this parent.
The correlation value between Yr and (Vr +Wr) was positively significant (r = 0.86) indicating that recessive alleles in the parents were responsible for increasing protein content.
McKendry et al. (1988) reported that protein content was mainly under the control of additive gene action. Singh et al. (1987) reported both additive and non additive gene action was important for this character.
Overall studies on gene action assessed through Vr/Wr graph analysis shows that the characters days to maturity, plant height, grains per spike, 1000-grains weight and protein content were controlled by partial dominance. The characters spikes per plant and spike length were controlled by over dominance. However epistatic gene action was noticed for the characters plant height, spikes per plant, spike length, grains per spike, 1000-grains weight, grain yield per plant and protein content. Among these gene actions partial dominance could easily be exploited through conventional breeding.
Therefore, the characters days to maturity, plant height, grains per spike, 1000-grains weight and protein content could be improved through bulk or pedigree selection practiced in the segregating generations. Since, there was non additive gene action for grain yield per plant, hence selection in early segregating generation would not be fruitful. Selection for this character is suggested in later generation after fixation of the alleles.