Research Article
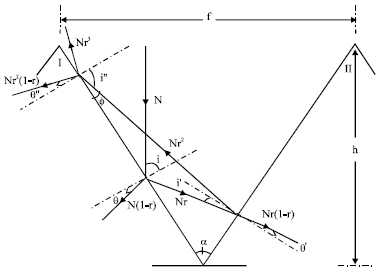
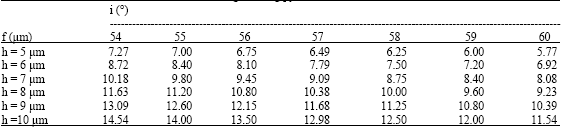
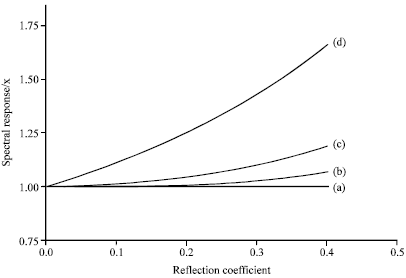
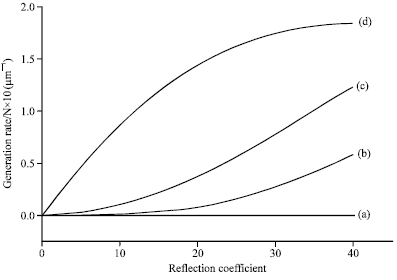
Modelisation of the Incident Solar Rays on the Textured Surface of the Solar Cells
Institut de Physique, Universite 08 mai 1945, Guelma 24000, Algerie
B. Hadjoudja
Laboratoire des Semiconducteurs, Departement de Physique, Universite Badji Mokhtar, Annaba, Algerie
B. Chouial
Laboratoire des Semiconducteurs, Departement de Physique, Universite Badji Mokhtar, Annaba, Algerie
A. Chibani
Laboratoire des Semiconducteurs, Departement de Physique, Universite Badji Mokhtar, Annaba, Algerie