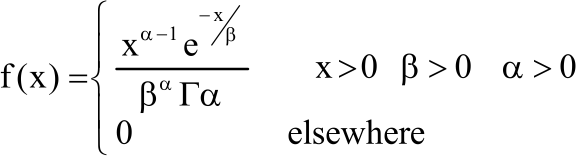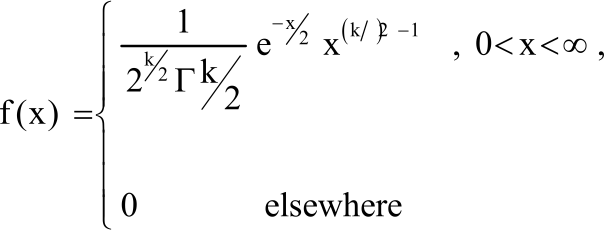Research Article
Probability of Type I Error and Power of Some Parametric Test: Comparative Approach
Department of Mathematical and Computing Sciences, Kola Daisi University, Ibadan, Nigeria
Biu O. Emmanuel
Department of Mathematics and Statistics, University of Port Harcourt, Port Harcourt, Nigeria
Otaru O.A. Paul
Department of Mathematics Sciences, Federal University Lokoja, Nigeria
LiveDNA: 234.31953