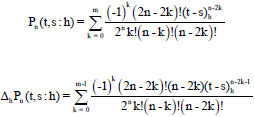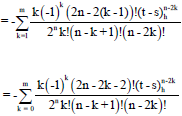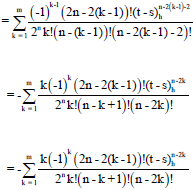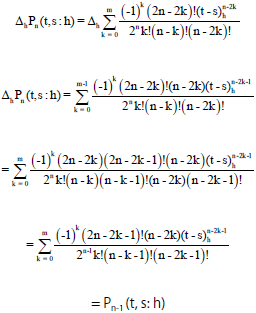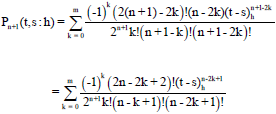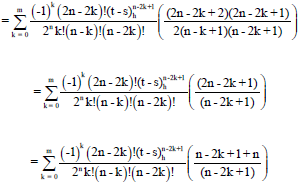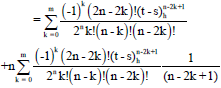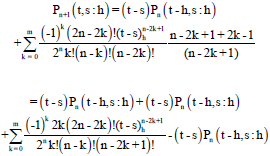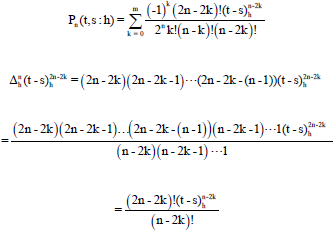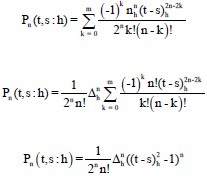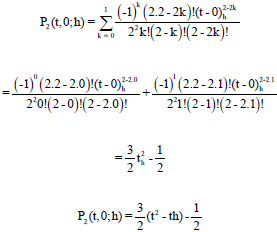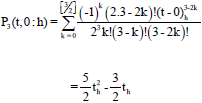Research Article
Basic Analogue of Legendre Polynomial and its Difference Equation
School of Mathematics and Allied Sciences, Jiwaji University Gwalior (M.P.), 474011, India
LiveDNA: 91.24911
Renu Jain
School of Mathematics and Allied Sciences, Jiwaji University Gwalior (M.P.), 474011, India