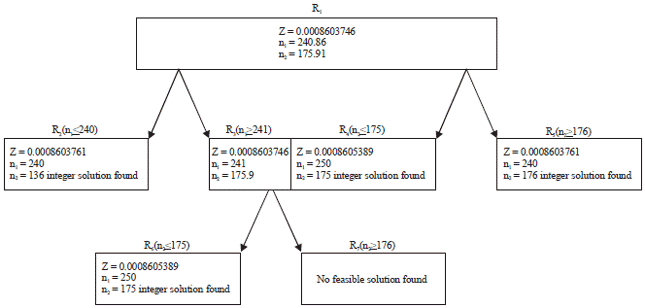
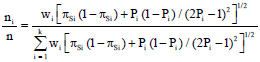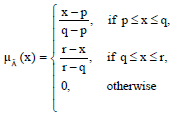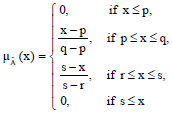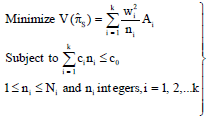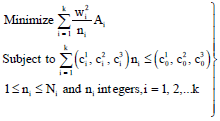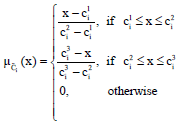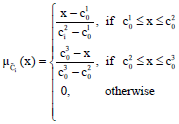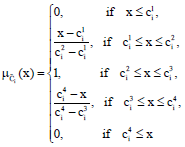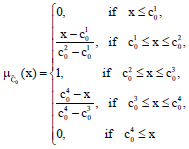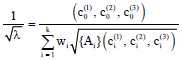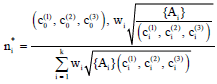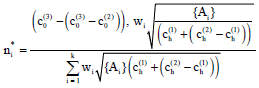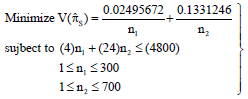Research Article
A New Approach to Randomized Response Model Using Fuzzy Numbers
Department of Mathematical Sciences, Islamic University of Science and Technology, Awantipora, Pulwama, 192122, Kashmir, India
LiveDNA: 91.6625
Peer Bilal
Department of Mathematical Sciences, Islamic University of Science and Technology, Awantipora, Pulwama, 192122, Kashmir, India
Muzafar Rasool
Department of Computer Science, Islamic University of Science and Technology, Awantipora, Pulwama, 192122, Kashmir, India