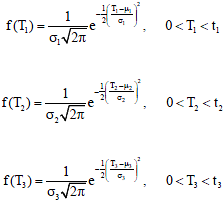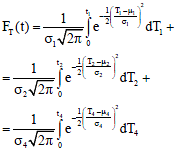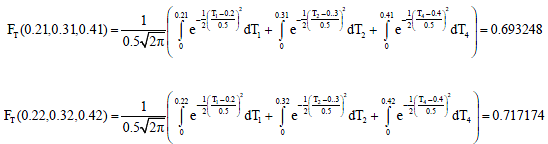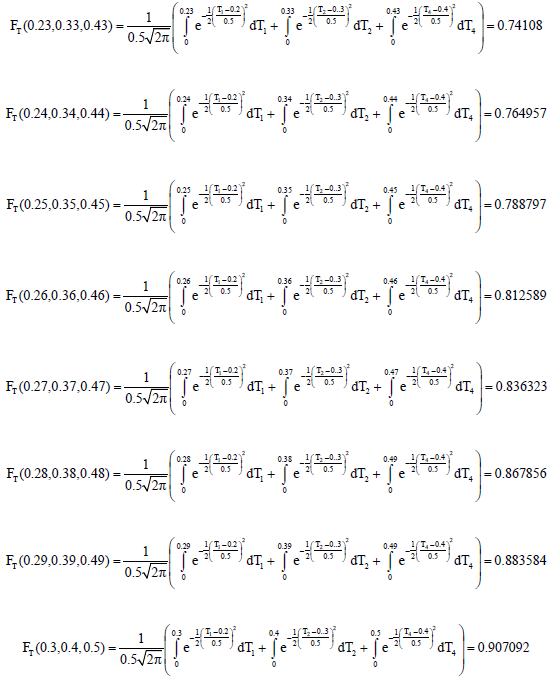Research Article
Joint Probability Distribution Function of the Repairing Time for the Defective Machines in the Multiple Queues System
Department of Mathematics, Faculty of Science, Port Said University, Port Said, Egypt
LiveDNA: 20.4959
ORCID: 0000-0002-4657-3045