Research Article
Perturbation Method as a Powerful Tool to Solve Highly Nonlinear Problems: The Case of Gelfand’s Equation
Electronic Instrumentation and Atmospheric Sciences School, Universidad Veracruzana, Circuito Gonzalo Aguirre Beltran S/N, Xalapa, Veracruz, 91000, Mexico
H. Vazquez-Leal
Electronic Instrumentation and Atmospheric Sciences School, Universidad Veracruzana, Circuito Gonzalo Aguirre Beltran S/N, Xalapa, Veracruz, 91000, Mexico
K. Boubaker
Ecole Superieure de Sciences et Techniques de Tunis, Universite de Tunis, Tunis, Permnent address: 63 Rue Sidi Jabeur 5100, Mahdia, Tunisia
Y. Khan
Department of Mathematics, Zhejiang University, Hangzhou 310027, China
A. Perez-Sesma
Electronic Instrumentation and Atmospheric Sciences School, Universidad Veracruzana, Circuito Gonzalo Aguirre Beltran S/N, Xalapa, Veracruz, 91000, Mexico
A. Sarmiento-Reyes
National Institute for Astrophysics, Optics and Electronics, Luis Enrique Erro #1, Sta. Maria Tonantzintla. Puebla, 72840, Mexico
V.M. Jimenez-Fernandez
Electronic Instrumentation and Atmospheric Sciences School, Universidad Veracruzana, Circuito Gonzalo Aguirre Beltran S/N, Xalapa, Veracruz, 91000, Mexico
A. Diaz-Sanchez
National Institute for Astrophysics, Optics and Electronics, Luis Enrique Erro #1, Sta. Maria Tonantzintla. Puebla, 72840, Mexico
A. Herrera-May
Micro and Nanotechnology Research Center, University of Veracruz, Calzada, Ruiz Cortines 455, Boca del Rio 94292, Veracruz, Mexico
J. Sanchez-Orea
National Institute for Astrophysics, Optics and Electronics, Luis Enrique Erro #1, Sta. Maria Tonantzintla. Puebla, 72840, Mexico
K. Pereyra-Castro
National Institute for Astrophysics, Optics and Electronics, Luis Enrique Erro #1, Sta. Maria Tonantzintla. Puebla, 72840, Mexico









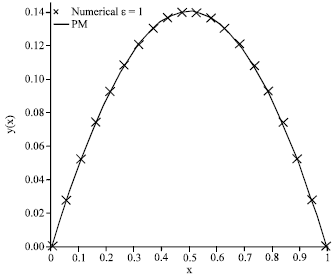
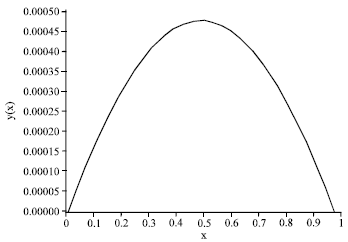
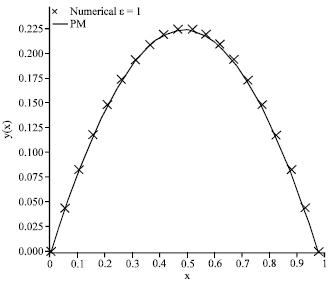
Alemnie Genaneh belew Reply
please dou help me about this topic?