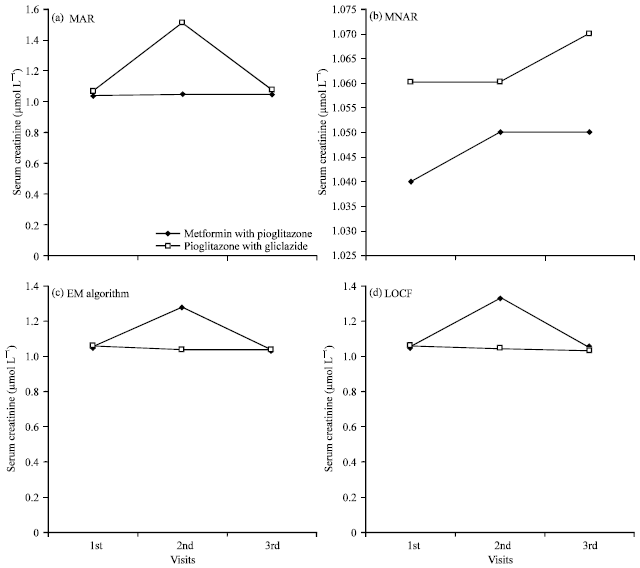
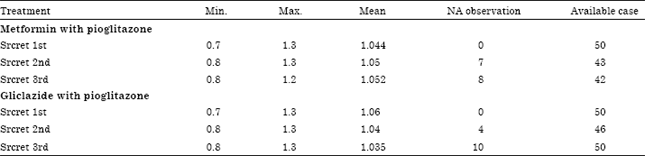
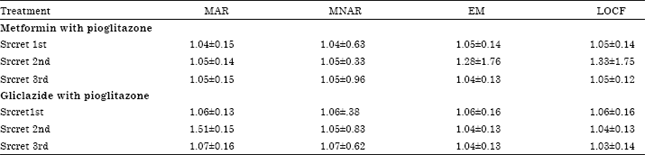
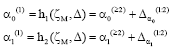Research Article
Pattern Mixture Modeling: An Application in Anti Diabetes Drug Therapy on Serum Creatinine in Type 2 Diabetes Patients
Department of Statistics, Gauhati University, Guwahati-781014, India
Atanu Bhattacharjee
Department of Statistics, Gauhati University, Guwahati-781014, India